Arguing about the magnetic force vector

[JD_PM]

I am writing about the nature of force in classical mechanics and what does really imply, in terms of change in motion. I am using as an example a circuit, on which we exert a force.

I am trying to justify the following scheme (concretely, $f_{mag}$):

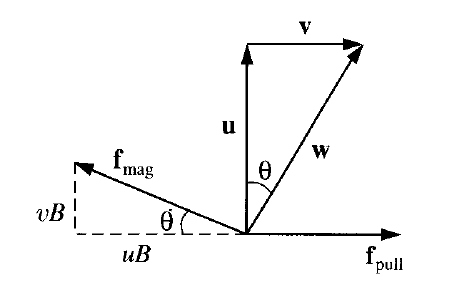
The thing is that I am wondering how can I justify $f_{mag}$ by using vector addition, based on Newton's Second Law (as neat as possible). I know that it can be justified by Lorentz Force Law (force has to be perpendicular to the displacement, as magnetic forces do not work) but that is not what I am looking for.

My idea is that, based on Newton's Second Law:

$$\vec F = m \frac{d \vec v}{dt}$$

We can argue that $\frac{d \vec v}{dt}$ is the change in velocity (final velocity - initial velocity) $w - u$, which yields the desired result for the direction of the force:

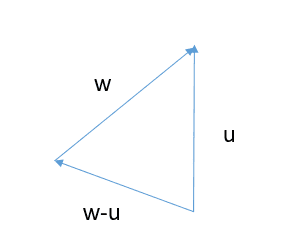
Do you see this as a valid argument?

Besides I am wondering how can I justify the constant m. I have been thinking about writing that once we subtract both vectors the constant m determines the force on each charge, but this sounds vague...

When I use this method (addition of vectors) with momentum instead of just velocities it's easy because I can justify the force vector by just subtracting two momentum vectors, as $\vec F = \frac{d \vec p}{dt}$ (I do not have to bother about any constant).

PS: Writing about Physics has recently become a hobby of mine. Actually this is a piece of a longer 'work' (I do it basically for fun) on explaining how optical tweezers work. As you can see I try to be kind of funny while writing XD. Any kind of advice will be really appreciated.

Thanks

 

[Henryk]

Firstly, no need to use vector addition rules, scalar equations are just fine.
Secondly, to understand what's happening when you pull a wire loop out in the presence of magnetic field, Newton's laws are not enough, you need electromagnetism, or at least Faraday's law of induction and Ohm's law.
Let me explain. Let's, for start, remove the resistor from the loop, i.e. make the loop open.
If you pull on the open loop, there will be an EMF induced in the loop, the value of which would be $EMF = \frac {d magnetic flux}{dt}$ but will there be any force? absolutely no. The loop is open, there is no current flowing and, therefore, no force.
Now, put the resistor back in and pull the loop again. Now, the induced EMF creates a current in the loop of the value $\frac {EMF}R$, the current flowing in the wire in the presence of the magnetic field creates Lorentz force which tends to oppose the direction of motion of the loop (Lenz law). How strong is the force? well, it depends on the value of the resistor. The smaller resistor, the bigger the current and the bigger the force.