Monoxdifly
MHB
- 288
- 0
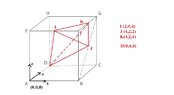
Given a cube ABCD.EFGH whose side length is 4 cm. If the point I, K, and J is dividing EF, FG, and BG to two equal lengths respectively, determine the volume of pyramid D.IJK!
I think I can work out the pyramid's base area by deriving for the formula of equilateral triangle area. What I can't is determine the pyramid's height. All I knew is that is must be less than 4√3 cm. Anyone willing to help me?
I think I can work out the pyramid's base area by deriving for the formula of equilateral triangle area. What I can't is determine the pyramid's height. All I knew is that is must be less than 4√3 cm. Anyone willing to help me?