chwala
Gold Member
- 2,828
- 423
- Homework Statement
- See attached
- Relevant Equations
- Kinematics
Find the question below;

For part (a), i used the graph to find ##t=22##

For part (b), i considered the points;
##(8,20)##, ##(13.333,20)## and ##(0,0)##
it follows that,
Area=##\sqrt {25.454(25.454-21.54)(25.454-24.036)(25.454-5.333)}##
##\sqrt {2842.58}##=##53.31##
There may be other better methods, my textbook only provides the final solution with no working...these are how the solutions look like (from textbook).
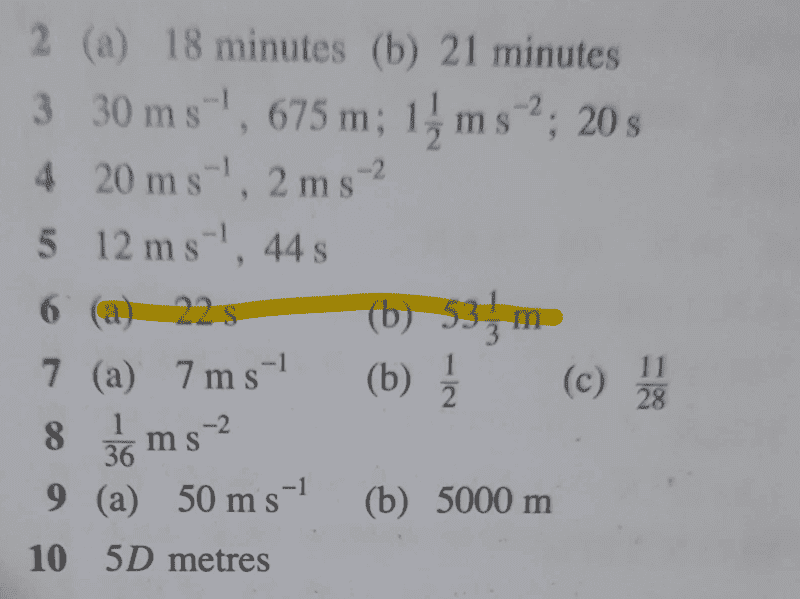
For part (a), i used the graph to find ##t=22##
For part (b), i considered the points;
##(8,20)##, ##(13.333,20)## and ##(0,0)##
it follows that,
Area=##\sqrt {25.454(25.454-21.54)(25.454-24.036)(25.454-5.333)}##
##\sqrt {2842.58}##=##53.31##
There may be other better methods, my textbook only provides the final solution with no working...these are how the solutions look like (from textbook).
Last edited: