- #1
tachi158
- 6
- 1
- TL;DR Summary
- Do particles veer towards objects because they encounter uneven clock rates, and they must maintain 4-velocity; since time is slower the space axes must compensate with acceleration. This causes path to veer towards decreasing clock rate.
Warning: Long post, apologies beforehand.
So science/physics isn't my field of study or work, but am always fascinated by it (looking back, perhaps I should have went down that route). In any event, a few months ago I went to finally learn more about relativity after reading a discussion of time dilation on the show, The Expanse. Actually, that curiosity led me to some pop-sci videos and a commenter said that the speed of light, really was just the speed of "causality." Never heard that term before so down the deep rabbit hole I went, trying to understand the basics of gravity without knowing the math.
I think I finally have a surface "general" understanding of SR and GR as I was completely blind before. But one thing I've been trying to figure out, is the mechanics(?) behind apparent gravitational attraction. I'm trying to clarify a video referenced on these forums, about a beaver with a clock on its head and feet. I've seen it mentioned that this was not accurate (point particles for example). So from what I understand (please correct me if I'm wrong, especially if I use the wrong terms).
Objects travel along a a straight worldline if no forces act upon it. In flat spacetime, it appears to be a straight line along the time axis(?) But in curved spacetime, it's a geodesic. It is mass/stress-energy bends spacetime. But it is the curvature of time that is mostly responsible for apparent gravitational attraction or gravitation. The curvature of space only comes into play with really massive objects and/or high velocity. Time dilation, gravitational redshift, is what I've read in sources (found on this forum) to describe the time curve (and how similar the results are to Newtonian gravity). And that curvature of time vs curvature of space is an artificial consideration. The curvature is of spacetime.
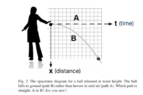
So my question: Imagine a point particle, traveling on it's worldline, in flat spacetime. No forces acting on it, no curved spacetime. Let's say it is moving though, in direction x. Let's say it travels in that direction for a sufficiently long time and it approaches a massive object ("MO"). A planet, sun, whatever. The MO is 45 degrees to the right. If the MO was not there, the particle's coordinate path is straight ahead (inertial frame). Because the MO bends spacetime, the inertial frame is now curved to the right, towards the object. Depending on the particle's relative velocity and position to the MO, it could just curve right and fly past it, go into orbit, or eventually crash into the MO. We all travel through our 4-velocity, which must maintain a constant magnitude (the more you travel through space, the less through time, etc.).
So a few things I have read: Geodesics is the longest proper time path between two points in spacetime. Or more accurately extremal, but in the case of objects it's usually maximal. And maximum proper time equates to the straightest path in 4D. But objects curve time, such that the closer you get to the MO, the less proper time there is, relative to farther distances from the MO. Gravitational time dilation. I've been trying to reconcile the two concepts which appears contradictory.
(1) Geodesics are the longest proper time path between two objects; (2) Geodesics of objects curve towards massive objects and increasingly travel through the area of slower time.
But perhaps I understood it wrong. A geodesic is just the path between two events, and this "longest proper time" thing has nothing to do with the curvature and apparent attraction. Massive object curves spacetime, particle moves towards the MO, and the path it takes will be the path of maximal proper time thereafter. Almost like that rule is ancillary, and not determinative.
An analogy I read from A.T. on this thread states
One explanation I found, which I find plausible, but want to double check was (my own words):
The time dilation/redshift/curvature of time causes uneven flow of time the further away you get from the mass. In flat space the flow of time is even on either side. An object at "rest" is still going through the time axis. You just cruise along on our 4-velocity headed straight up the time vector. When spacetime is curved, the time axis is no longer orthogonal to the space axes. There is a mixture. You really can't be at rest any more even if you tried. Why? The 4-velocity must be conserved as the speed of light c. So as time goes slower, the space axes of the 4-velocity must compensate to maintain it.
So when you encounter uneven clock-rate gradients, you get pulled in and must accelerate to maintain the 4-velocity. This acceleration has the direction of decreasing clock rate.
Sounds similar to "veering towards slower time/denser spacetime." Like a plane that is in flat spacetime, approaches that MO from earlier. The right wing encounters the slower clockrate first, gets pulled in, must accelerate to maintain 4-velocity, so on and so forth and depending on velocity and trajectory, is now crashing into earth (or orbiting, etc).
Is this accurate?
So science/physics isn't my field of study or work, but am always fascinated by it (looking back, perhaps I should have went down that route). In any event, a few months ago I went to finally learn more about relativity after reading a discussion of time dilation on the show, The Expanse. Actually, that curiosity led me to some pop-sci videos and a commenter said that the speed of light, really was just the speed of "causality." Never heard that term before so down the deep rabbit hole I went, trying to understand the basics of gravity without knowing the math.
I think I finally have a surface "general" understanding of SR and GR as I was completely blind before. But one thing I've been trying to figure out, is the mechanics(?) behind apparent gravitational attraction. I'm trying to clarify a video referenced on these forums, about a beaver with a clock on its head and feet. I've seen it mentioned that this was not accurate (point particles for example). So from what I understand (please correct me if I'm wrong, especially if I use the wrong terms).
Objects travel along a a straight worldline if no forces act upon it. In flat spacetime, it appears to be a straight line along the time axis(?) But in curved spacetime, it's a geodesic. It is mass/stress-energy bends spacetime. But it is the curvature of time that is mostly responsible for apparent gravitational attraction or gravitation. The curvature of space only comes into play with really massive objects and/or high velocity. Time dilation, gravitational redshift, is what I've read in sources (found on this forum) to describe the time curve (and how similar the results are to Newtonian gravity). And that curvature of time vs curvature of space is an artificial consideration. The curvature is of spacetime.
So my question: Imagine a point particle, traveling on it's worldline, in flat spacetime. No forces acting on it, no curved spacetime. Let's say it is moving though, in direction x. Let's say it travels in that direction for a sufficiently long time and it approaches a massive object ("MO"). A planet, sun, whatever. The MO is 45 degrees to the right. If the MO was not there, the particle's coordinate path is straight ahead (inertial frame). Because the MO bends spacetime, the inertial frame is now curved to the right, towards the object. Depending on the particle's relative velocity and position to the MO, it could just curve right and fly past it, go into orbit, or eventually crash into the MO. We all travel through our 4-velocity, which must maintain a constant magnitude (the more you travel through space, the less through time, etc.).
So a few things I have read: Geodesics is the longest proper time path between two points in spacetime. Or more accurately extremal, but in the case of objects it's usually maximal. And maximum proper time equates to the straightest path in 4D. But objects curve time, such that the closer you get to the MO, the less proper time there is, relative to farther distances from the MO. Gravitational time dilation. I've been trying to reconcile the two concepts which appears contradictory.
(1) Geodesics are the longest proper time path between two objects; (2) Geodesics of objects curve towards massive objects and increasingly travel through the area of slower time.
But perhaps I understood it wrong. A geodesic is just the path between two events, and this "longest proper time" thing has nothing to do with the curvature and apparent attraction. Massive object curves spacetime, particle moves towards the MO, and the path it takes will be the path of maximal proper time thereafter. Almost like that rule is ancillary, and not determinative.
An analogy I read from A.T. on this thread states
That seems similar so the two clocks analogy, but perhaps instead of on it's head and feet, it's above the head, and below the feet. But why does it steer towards the area of slower time? If objects like to linger in areas of faster proper time, why does the object veer down to areas of slower time?The rock advancing trough spacetime steers towards the area of slower time(~=denser spacetime), similar to a light ray advancing trough a medium with varying optical density also steers towards the area of higher optical density.
One explanation I found, which I find plausible, but want to double check was (my own words):
The time dilation/redshift/curvature of time causes uneven flow of time the further away you get from the mass. In flat space the flow of time is even on either side. An object at "rest" is still going through the time axis. You just cruise along on our 4-velocity headed straight up the time vector. When spacetime is curved, the time axis is no longer orthogonal to the space axes. There is a mixture. You really can't be at rest any more even if you tried. Why? The 4-velocity must be conserved as the speed of light c. So as time goes slower, the space axes of the 4-velocity must compensate to maintain it.
So when you encounter uneven clock-rate gradients, you get pulled in and must accelerate to maintain the 4-velocity. This acceleration has the direction of decreasing clock rate.
Sounds similar to "veering towards slower time/denser spacetime." Like a plane that is in flat spacetime, approaches that MO from earlier. The right wing encounters the slower clockrate first, gets pulled in, must accelerate to maintain 4-velocity, so on and so forth and depending on velocity and trajectory, is now crashing into earth (or orbiting, etc).
Is this accurate?