- #1
Muthumanimaran
- 81
- 2
Recently I lend the Classical mechanics book written by Goldstein from the library, In the last page, someone scribbled this problem without any solution, I am just curious and want to give a try the problem mentioned below. I just want to know whether my approach and my solution is correct or not.
1. Homework Statement
Find the Time period of the particle confined to the Potential energy of the form $V(x)=-\frac{V_{0}}{\cosh^2(\alpha{x})}$.
$$\int_{0}^{t_0}dt=\int_{x_0}^{x}\frac{dx}{\sqrt{\frac{2}{m}(E-V(x))}}$$
Where $'E'$ is the Total Energy
and $'m'$ is the mass of the particle
Since the potential energy is negative, the total Energy required to escape from the potential is zero, i.e, $E=0$,
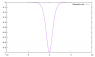
The Potential diagram is attached with this thread, as we can see, the potential goes to 0 as $x$ goes to $\infty$
or $-\infty$, If I take one half of the Potential say from $0$ to $\infty$ and substituting in the above integral becomes,
$$\int_{0}^{\frac{T}{2}}dt=\sqrt{\frac{m}{2V_0}}\int_{0}^{\infty}cosh(\alpha{x})dx$$
Apparently the right hand side goes to infinity. And the time period of the particle confined also goes to infinity. Am I right? I solved the problem but I don't know whether my solution is correct or not. Is there any mistake in my solution?
1. Homework Statement
Find the Time period of the particle confined to the Potential energy of the form $V(x)=-\frac{V_{0}}{\cosh^2(\alpha{x})}$.
Homework Equations
$$\int_{0}^{t_0}dt=\int_{x_0}^{x}\frac{dx}{\sqrt{\frac{2}{m}(E-V(x))}}$$
Where $'E'$ is the Total Energy
and $'m'$ is the mass of the particle
The Attempt at a Solution
Since the potential energy is negative, the total Energy required to escape from the potential is zero, i.e, $E=0$,
The Potential diagram is attached with this thread, as we can see, the potential goes to 0 as $x$ goes to $\infty$
or $-\infty$, If I take one half of the Potential say from $0$ to $\infty$ and substituting in the above integral becomes,
$$\int_{0}^{\frac{T}{2}}dt=\sqrt{\frac{m}{2V_0}}\int_{0}^{\infty}cosh(\alpha{x})dx$$
Apparently the right hand side goes to infinity. And the time period of the particle confined also goes to infinity. Am I right? I solved the problem but I don't know whether my solution is correct or not. Is there any mistake in my solution?
Attachments
Last edited: