SUMMARY
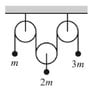
The discussion focuses on solving the dynamics of an Atwood machine with three masses: m, 2m, and 3m. The key equations derived include a1 = (mg + T)/m, a2 = (2mg + 2T)/2m, and a3 = (3mg + T)/3m, leading to accelerations of -1/5mg for the first two masses and 3/5mg for the third. The tension in the string remains constant due to the assumption of massless pulleys and neglecting friction. A critical insight is the need to express the total string length as a function of the displacements to solve for the system's accelerations accurately.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with free body diagrams
- Knowledge of tension in strings and its implications in pulley systems
- Ability to differentiate functions and apply constraints in physics problems
NEXT STEPS
- Study the derivation of equations of motion for Atwood machines
- Learn about constraints in mechanical systems and their mathematical representations
- Explore the implications of tension in multi-mass pulley systems
- Review differentiation techniques in the context of physics problems
USEFUL FOR
Physics students, educators, and anyone interested in classical mechanics, particularly in understanding the dynamics of pulley systems and forces acting on multiple masses.