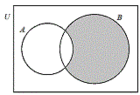
The discussion revolves around the interpretation and calculation involving a Venn diagram with a universal set U and subsets A and B. Participants explore set operations, specifically the union and intersection of sets, and their implications in terms of probabilities.
There appears to be agreement on the correctness of the probability calculation involving $B\cup A'$, but the overall discussion does not reach a consensus on the broader implications or interpretations of the set operations.
The discussion does not clarify the definitions of the sets A and B or the context of the universal set U, which may affect the interpretations of the expressions used.
| (c) $\displaystyle\frac{n(B\cup A')}{n(U)}=\frac{35}{100}=\frac{7}{20}$ |
karush said:
