LLT71
- 73
- 5
I found it somehow tricky to understand average speed and average power in mathematical fashion.
I suppose general idea of taking average of some quantity is: sum of all values/number of values.
how that idea fit's into idea of average speed=distance traveled/time traveled
similarly, average signal power:
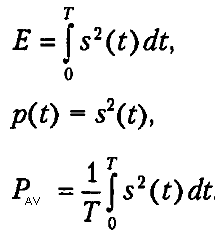
why is it over T?
I suppose general idea of taking average of some quantity is: sum of all values/number of values.
how that idea fit's into idea of average speed=distance traveled/time traveled
similarly, average signal power:
why is it over T?