Averaging oscilloscope traces (statistics)

[roam]

Homework Statement

I am trying to find the best method to determine the average constant spacing between the consecutive dips in the following oscilloscope traces.

Relevant Equations

$$\frac{\sigma_{N}}{\sqrt{N}}$$

I have collected a large number of oscilloscope traces (these relate to the modes of a laser cavity). Four sets are shown here:

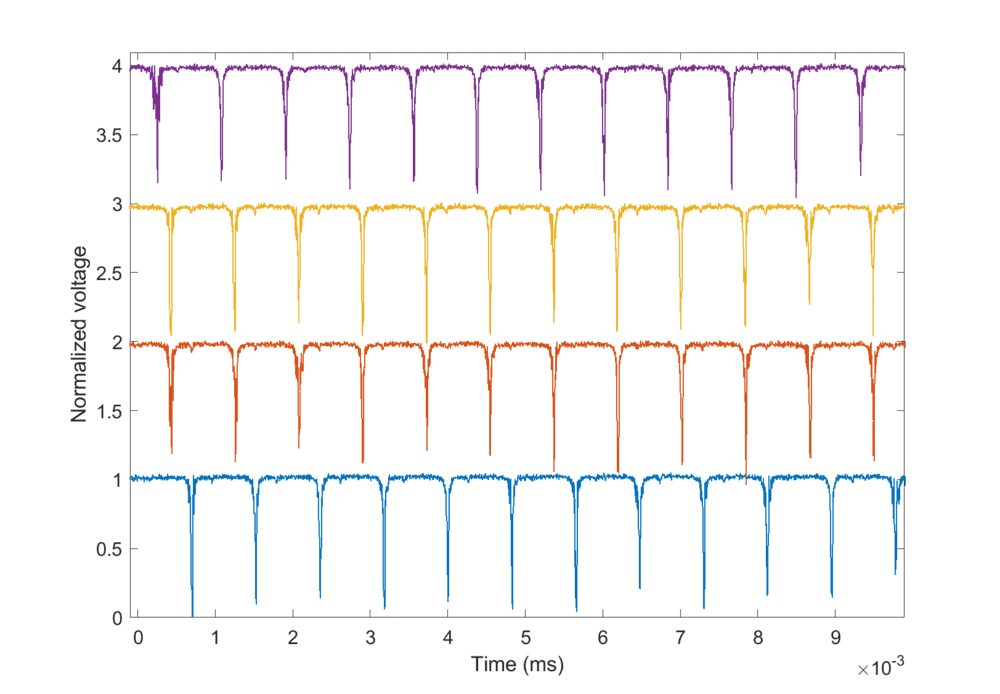
There are two ways for finding the average spacing $\Delta t$ between the adjacent dips:

1. Measure all the individual $\Delta t$s from each measurement separately and then average everything together.

2. Combine all the measurements into one single curve by averaging them. Then we only have 11 $\Delta t$s to calculate and average into a single value. This seems to be a quicker method, but a problem with this is that the traces slightly vary in time so the position of the dips do not perfectly coincide (they have to be offset manually).

I believe the estimated error in the average will be given by $\frac{\sigma_{N}}{\sqrt{N}}$. So, which method is more reliable, and how would the errors vary depending on the method?

Any explanation would be greatly appreciated.

 

[Ray Vickson]

I have collected a large number of oscilloscope traces (these relate to the modes of a laser cavity). Four sets are shown here:

View attachment 241062

There are two ways for finding the average spacing $\Delta t$ between the adjacent dips:

1. Measure all the individual $\Delta t$s from each measurement separately and then average everything together.

2. Combine all the measurements into one single curve by averaging them. Then we only have 11 $\Delta t$s to calculate and average into a single value. This seems to be a quicker method, but a problem with this is that the traces slightly vary in time so the position of the dips do not perfectly coincide (they have to be offset manually).

I believe the estimated error in the average will be given by $\frac{\sigma_{N}}{\sqrt{N}}$. So, which method is more reliable, and how would the errors vary depending on the method?

Any explanation would be greatly appreciated.

Quite possibly the best approach is to look at this problem as a so-called "analysis of variance" (ANOVA) case.

You have 44 data items, arranged in four groups of 11 each. However, each group of 11 is measured under a difference in some underlying input parameter (normalized voltage). Possibly the different groups are not all the same; perhaps their (11-item) averages are different because of some underlying systematic effect, or maybe the computed differences are just due to random chance and there is no true underlying difference between them. That is the question you would like to answer, and using ANOVA is a common approach.

I won't try to present the formulas and concept here; they appear in introductory Statistics textbooks, or nowadays in freely-accessible web pages. Just Google "ANOVA".

 

[roam]

Hi @Ray Vickson

For each of the four data sets, we had the following averages over all 11 items:

$$
\begin{array}{c|c}
\text{Measurement group} & \text{Mean}\ \Delta t\ (\mu s)\\
\hline 1 & 0.824\\
2 & 0.824\\
3 & 0.825\\
4 & 0.825
\end{array}
$$

I applied the one-way ANOVA to my data using Matlab and it produced the following table:

I believe the null hypothesis is that the samples are taken from populations with the same mean. If I am not mistaken, the large p-value of 0.98 indicates that differences between group means are not significant. So, what does this tell us about the experiment? Does that mean the differences are purely due to random noise?

If I want to quote a single value for $\Delta t$, should I simply average all four means?

 

[Ray Vickson]

Hi @Ray Vickson

For each of the four data sets, we had the following averages over all 11 items:

$$
\begin{array}{c|c}
\text{Measurement group} & \text{Mean}\ \Delta t\ (\mu s)\\
\hline 1 & 0.824\\
2 & 0.824\\
3 & 0.825\\
4 & 0.825
\end{array}
$$

I applied the one-way ANOVA to my data using Matlab and it produced the following table:

View attachment 241403

I believe the null hypothesis is that the samples are taken from populations with the same mean. If I am not mistaken, the large p-value of 0.98 indicates that differences between group means are not significant. So, what does this tell us about the experiment? Does that mean the differences are purely due to random noise?

If I want to quote a single value for $\Delta t$, should I simply average all four means?

What the large p-value tells you is, basically, there is no evidence for any systematic effect due to applied voltage. It looks like the four samples could very well be coming from a common, underlying distribution, and that, yes, indeed, the differences could be due to random noise.

Part of the problem may be that your sample sizes are not very large and that your data itself is highly "regular", without large random fluctuations. If you had 4400 or 44,000 samples instead of only 44, you might be able to pick out some genuine differences.

If you are willing to say that all four samples are from the same population, your best way of estimating $\Delta t$ would be to use the single sample of size 44 to do your estimations.