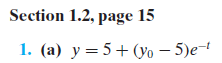MHB How Do Boundary Conditions Affect Differential Equations?
- Thread starter karush
- Start date
Click For Summary
Boundary conditions play a crucial role in solving differential equations, as they help determine arbitrary constants in the general solution. The discussion centers on the differential equation dy/dt = 2y - 5, which is rewritten and solved using an integrating factor. The integration process reveals that the solution can be expressed in terms of the initial condition y(0) = y_0, leading to the final form of the solution. Participants emphasize the importance of verifying solutions against the original differential equation to ensure accuracy. Understanding how boundary conditions influence the constants in solutions is essential for grasping the overall behavior of the system described by the differential equation.
Similar threads
- · Replies 5 ·
- · Replies 7 ·
- · Replies 6 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 4 ·
- · Replies 9 ·
- · Replies 3 ·