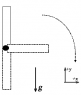
- #1
natasha13100
- 58
- 0
Homework Statement
This is actually a multi-part question, but I only need help on the following part right now.
A uniform bar of mass m and length L is pivoted at one end and is held vertically as shown. After the bar is released, it swings downward with no friction in the pivot.
At the instant the bar is at the bottom of the swing, find the magnitudes of the angular velocity and angular acceleration.
I have no problem finding angular velocity. I use the following symbols:
t=torque
Ip=moment of inertia of the pivot
a=tangential acceleration
v=tangential velocity
α=angular acceleration
ω=angular velocity
K=kinetic energy
U=potential energy
Homework Equations
for sure:
Ip=1/3mL2
Ui+Ki=Ktrans,f+Krot,f+Uf
Ugrav=mgh
Ktrans=1/2mv2
Krot=1/2Iω2
maybe:
t=rFsinθ
t=Iα
a=Rα
F=G+t
G=mg
Icm=1/12mL2
The Attempt at a Solution
Ui=mgL/2
Uf=-mgL/2
Ki=0
Ktrans,f=0
Krot,f=1/2Ipω2=1/6mL2ω2
mgL=1/6mL2ω2
6g/L=ω2
ω=√(6g/L)
mg=Ipα
α=mg/Ip=mg/(1/3mL2)=3g/L2
Attachments
Last edited: