Basic Quantum Circuit: States of Individual Qubits

[cwill53]

Homework Statement

For the teleportation quantum circuit below starting with $|000\rangle$ as $|q_2 q_1 q_0\rangle$:

A. Reproduce the quantum circuit in QISKIT with the result. (screenshot the results)

B. Label both the quantum and classical registers after each operation as previously shown in the recorded notes.

C. Store the Step 1b measurement result in the 0th classical qubit and store Step 3 measurement result in the 1st classical qubit. How should we modify the conditional CNOT and Z-gates in Step 1b and Step 3 so it will produce the same result? Reproduce in QISKIT.

D. For this example, why is the state of the original electron destroyed? How is it related to the no-cloning theorem? If Alice’s state was $|0\rangle$ , do we need quantum teleportation to transfer the state?

Relevant Equations

$$|0\rangle=\begin{bmatrix}
1\\
0
\end{bmatrix}$$

$$|1\rangle=\begin{bmatrix}
0\\
1
\end{bmatrix}$$

$$H=\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1\\
1& -1
\end{bmatrix}$$

$$U_{\textup{XOR}}=\begin{bmatrix}
1 & 0 &0 &0 \\
0& 1& 0 &0 \\
0 &0 & 0 & 1\\
0& 0 & 1 & 0
\end{bmatrix}$$

$$I=\begin{bmatrix}
1 &0 \\
0& 1
\end{bmatrix}$$

$$Z=\begin{bmatrix}
1 &0 \\
0& -1
\end{bmatrix}$$

I have done part A so far below, but I'm a bit behind on my reading, so I don't quite understand the action of the controlled-NOT gate on a single qubit.

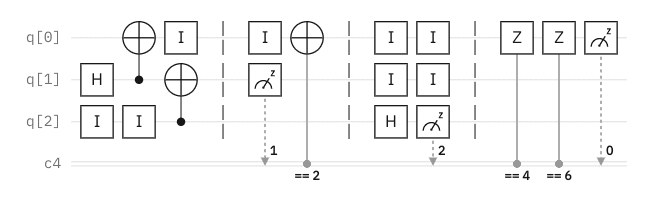
What I have so written so far for part B is:

Let $\mathcal{H}=(\mathbb{C}^2)^{\otimes 3}$. Let $|\psi _{q_i}\rangle_k$ , $(i\in\left \{ 0,1,2 \right \})$ be the state of the $i$-th qubit in the register after the action of the $k$-th gate along the wire carrying the $i$-th qubit. Since the initial state of each qubit is $|0\rangle=\begin{bmatrix} 1 & 0 \end{bmatrix}^T$, we have

$$

|\psi _{q_1}\rangle_1=H|0\rangle=\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1\\
1& -1
\end{bmatrix}\begin{bmatrix}
1\\
0
\end{bmatrix}=\frac{1}{\sqrt{2}}\begin{bmatrix}
1\\
1
\end{bmatrix}
$$

Since I'm behind on my readings, I'm a bit confused as to the action of the controlled-NOT gate and how it changes both the state of the control and target qubit. I was hoping someone could walk me through this problem.

 

[.Scott]

Since I'm behind on my readings, I'm a bit confused as to the action of the controlled-NOT gate and how it changes both the state of the control and target qubit. I was hoping someone could walk me through this problem.

Entanglements not withstanding, the CNOT does not change the control qubit. They will invert the state of the target qubit for conditions where the control bit is "high" or "up" or "1" (your choice of the symbol set).

The reason I say "entanglements not withstanding", is that entangled qubits don't really have individual states. Instead, until measured, the entangled system of qubits has a single state that can be described by all of the possible qubits state combinations and their probabilities.

In this case, the possible combinations of xy are 00, 01, 10, and 11.
If the probabilities of these four states are a, b, c, and d respectively, then the state of the system is specified as: a00> + b01> + c10> + d11>
applying CNOT with x as control and y as target, you would get: a00> + b01> + d10> + c11>

In the sense that the state of x goes from (a+b)0> + (c+d)1> to (a+b)0> + (d+c)1>, x (the control qubit) does not change states.

In contrast, y (the target qubit) will go from (a+c)0> + (b+d)1> to (a+d)0> + (b+c)1>.

But you need to exercise caution when computing the individual qubit probabilities of an entangled system because only the system description a00> + b01> + c10> + d11> fully describes the system state.

 

[cwill53]

Entanglements not withstanding, the CNOT does not change the control qubit. They will invert the state of the target qubit for conditions where the control bit is "high" or "up" or "1" (your choice of the symbol set).

The reason I say "entanglements not withstanding", is that entangled qubits don't really have individual states. Instead, until measured, the entangled system of qubits has a single state that can be described by all of the possible qubits state combinations and their probabilities.

In this case, the possible combinations of xy are 00, 01, 10, and 11.
If the probabilities of these four states are a, b, c, and d respectively, then the state of the system is specified as: a00> + b01> + c10> + d11>
applying CNOT with x as control and y as target, you would get: a00> + b01> + d10> + c11>

In the sense that the state of x goes from (a+b)0> + (c+d)1> to (a+b)0> + (d+c)1>, x (the control qubit) does not change states.

In contrast, y (the target qubit) will go from (a+c)0> + (b+d)1> to (a+d)0> + (b+c)1>.

But you need to exercise caution when computing the individual qubit probabilities of an entangled system because only the system description a00> + b01> + c10> + d11> fully describes the system state.

I'm still pretty confused as to what exactly I need to do for this problem. I'm trying to figure out what the state of the entire system should be after Step 1a, but it doesn't quite make sense to me. I have

$$

|\psi _{1a}\rangle=(I\otimes_K I)U_{\textup{CNOT}}(H|0 \rangle\otimes_K|0 \rangle )\otimes_KU_{\textup{CNOT}}(II|0 \rangle\otimes_KH|0 \rangle )
$$

but when I actually compute this I get a 16-dimensional vector, when I know the entangled system should live in an 8-dimensional vector space.

 

[cwill53]

Entanglements not withstanding, the CNOT does not change the control qubit. They will invert the state of the target qubit for conditions where the control bit is "high" or "up" or "1" (your choice of the symbol set).

The reason I say "entanglements not withstanding", is that entangled qubits don't really have individual states. Instead, until measured, the entangled system of qubits has a single state that can be described by all of the possible qubits state combinations and their probabilities.

In this case, the possible combinations of xy are 00, 01, 10, and 11.
If the probabilities of these four states are a, b, c, and d respectively, then the state of the system is specified as: a00> + b01> + c10> + d11>
applying CNOT with x as control and y as target, you would get: a00> + b01> + d10> + c11>

In the sense that the state of x goes from (a+b)0> + (c+d)1> to (a+b)0> + (d+c)1>, x (the control qubit) does not change states.

In contrast, y (the target qubit) will go from (a+c)0> + (b+d)1> to (a+d)0> + (b+c)1>.

But you need to exercise caution when computing the individual qubit probabilities of an entangled system because only the system description a00> + b01> + c10> + d11> fully describes the system state.

I've figured out the state of the system at the first barrier. It's
$$|q_2q_1q_0\rangle=\frac{1}{\sqrt{2}}(|000\rangle+|011\rangle)$$
I'm stuck trying to find what happens to the state of the system and what's read onto the classical register as a result of the measurement of the state in the first time slice after the first barrier.