Belt and Pulleys - Centrifugal Forces

[MPavsic]

Hi.

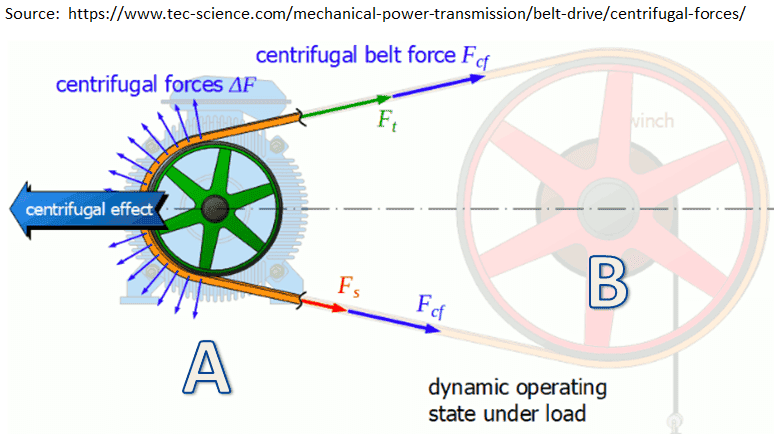
• I assume that vector summation of the centrifugal forces acting on the belt, on pulley A and B, equals to zero. Is Centrifugal force on pulley A static or dynamic force?
• What would, hypothetically, happen if the sum centrifugal forces acting on the belt are not zero? Could some kind of arrangement, of the belt and pulleys, be used as a propulsion system if vector summation of centrifugal forces acting on the belt on all pulleys doesn’t equal to zero?

 

[A.T.]

Is Centrifugal force on pulley A static or dynamic force?

Here it is an inertial force (in the D'Alembert sense, not in the non-inertial frame sense).

 

[MPavsic]

Here it is an inertial force

Is Centrifugal force kind of dynamic force, or is it more on side of static force, if the belt is traveling with constant velocity over the pulleys?
What if the vector sum of centrifugal forces of the belt is not equal to zero? Can such configuration of the belt and pulleys cause the acceleration of the device mass center, violating third Newton Law?

 

[sophiecentaur]

Summary: static force; dynamic force

if the sum centrifugal forces acting on the belt are not zero?

For this to occur, the belt would need to slip because it leaves the surface. See this link which shows the effect with a chain. There is no normal force from the edge of the beaker. The weight of the chain causes it to fall and the centrifugal force accounts for the radius of the curve.

 

[MPavsic]

the belt would need to slip because it leaves the surface

In my theoretical model, the belt does not leave the surface of the pulley, because it is pre tensioned. The calculation model shows that vector sum of centrifugal forces of the belt is not equal to zero. The belt centrifugal forces on the pulleys are compensated in the belt tension. The belt tension is influencing the mass center of the device which should start to move, if the centrifugal forces of the belt are kind of dynamic forces.
The belt and pulleys are arranged in 3D space.

 

[jrmichler]

The belt pretension causes a normal force between the belt and pulley. Centrifugal force is opposite to that normal force, so subtracts from the normal force due to pretension. The centrifugal force is calculated from the mass of the belt, the velocity of the belt, and the radius of the pulley. If the centrifugal force is high enough, the belt will float over the pulley without contacting the pulley. Note that all belts are elastic, so the tension can change when it is running.

Remember that there is a minimum net tension on the slack side to drive the load, which you calculate from the belt friction equation (search the term). Note also that the belt friction equation assumes that there is enough normal force and friction to prevent slipping. That's another necessary calculation.

I learned this lesson the hard way when one of my ideas did not work. But that is a story for another time.

 

[A.T.]

... violating third Newton Law?

No.

 

[sophiecentaur]

In my theoretical model, the belt does not leave the surface of the pulley, because it is pre tensioned.

If your model insists on 'enough' tension to maintain contact then doesn't that exclude the net centrifugal forces being non zero?

Aamof, your original statement of the situation is a bit too vague and I am not too sure about your definition. What centrifugal forces are you actually discussing? My link about the chain waterfall shows a temporary equilibrium situation where the radius of the curve is just right to balance the two tensions.

 

[MPavsic]

If your model insists on 'enough' tension to maintain contact then doesn't that exclude the net centrifugal forces being non zero?

This is a good question that I am not able to answer directly. My explanation would be:

• Centrifugal force is some kind of dynamic force as shown in your suggested video (lifting the chain from a jar)
• For the belt particles when they are circling around instant center of rotation, I can freely use the kinematic equations of rigid rotating body.
• The belt, when circling over pulleys will (theoretically) create super elastic collision with pulleys (angular momentum of the belt is conserved).

The question is; will the friction between the belt and pulleys prevent compensation of the belt tension created by centrifugal forces on the belt. (But centrifugal forces of the belt cannot just disappear)

Jrmichler, I will do your prescribed homework soon.

I am dancing around this problem quite some time, beside problems with patent clerk; I decided to go public as far as I safely can to solve this mystery. I am a self-learner.

 

[MPavsic]

Note also that the belt friction equation assumes that there is enough normal force and friction to prevent slipping

I did shorter research.
In my model the preload tension is just enough to run just a belt over the pulleys with constant speed. The idea is that friction is necessary only on the driving pulley. The load on the belt is represented only by belt itself and some additional load is created when the belt is crossing from one pulley to another at very shallow angles (5deg in average, total sum of crossings = 90deg.).
In the model I have calculated absolute acceleration of the belt particles. That include:
- Vector sum of normal forces (centripetal accelerations) of the belt when running over pulleys.
- Vector sum of ‘Collisions’ when the belt touches the pulley and leaves the pulley at shallow angles.
The result is that vector sum of absolute acceleration of the belt on driving pulley is greater than vector sum of absolute accelerations of the belt on the other 3D positioned pulleys.
The article “Preload with consideration of centrifugal forces” is explaining that centrifugal compensating forces in the belt are always present regardless to amount of friction between the pulley and the belt.
Is my thinking correct?

 

[sophiecentaur]

But centrifugal forces of the belt cannot just disappear

Why not? As soon as a section of the belt stops circular motion, there is no centrifugal force.

centrifugal compensating forces in the belt are always present regardless to amount of friction between the pulley and the belt.

The centrifugal force is only dependent on the mass, the radius of rotation and the angular velocity. Also, friction forces are orthogonal to the centrifugal forces. That chain example has circular motion without any friction.

 

[MPavsic]

The centrifugal force is only dependent on the mass, the radius of rotation and the angular velocity

Thank you for your sincere answers.