etotheipi
I was reading through a set of notes and found something a little odd. The aim is to solve the beam structure shown below, which is massless and of length ##l##.
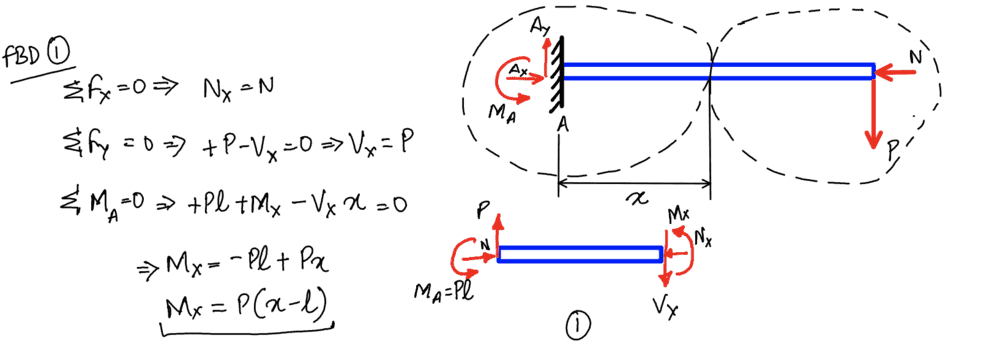
By considering the beam as a whole, we obtain ##A_y = P##, ##A_x = N## and by taking moments about A we see ##M_A = Pl##.
However, now we consider a segment of the beam up to a distance ##x## along its length. We define the reaction forces and internal bending moments at this point to be ##N_x##, ##V_x## and ##M_x## as shown. The ##\sum F_x## and ##\sum F_y## parts are fine, but I wonder how they justify their third equation?
As far as I am aware, the internal bending moment at any point in the beam is taken about an axis passing through that point (N.B. we can really define 3 bending moments, but in this problem we only need the 1), like this:
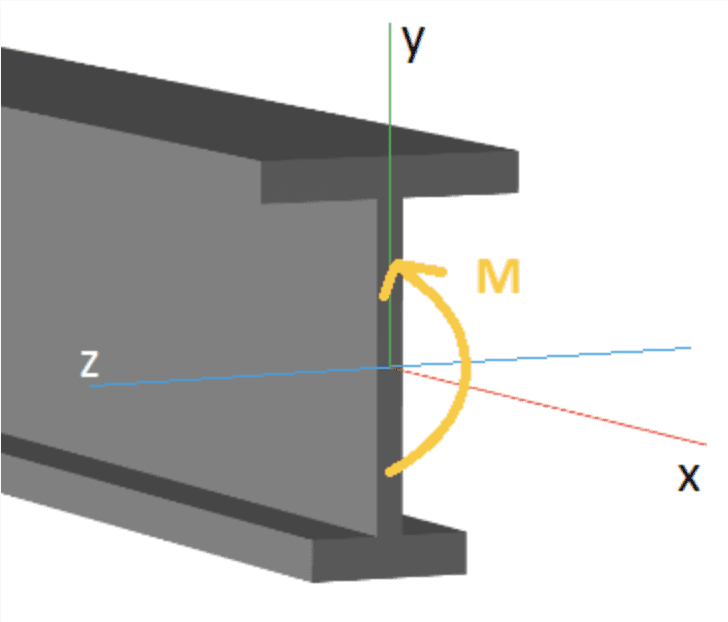
##M_A## is taken about one axis, and ##M_x## is taken about another parallel axis displaced from the first axis by a distance ##x##. But when balancing torques, it only makes sense to add torques about the same axis!
I wondered then, why they used two torques about different axes in the same expression? Thanks!
By considering the beam as a whole, we obtain ##A_y = P##, ##A_x = N## and by taking moments about A we see ##M_A = Pl##.
However, now we consider a segment of the beam up to a distance ##x## along its length. We define the reaction forces and internal bending moments at this point to be ##N_x##, ##V_x## and ##M_x## as shown. The ##\sum F_x## and ##\sum F_y## parts are fine, but I wonder how they justify their third equation?
As far as I am aware, the internal bending moment at any point in the beam is taken about an axis passing through that point (N.B. we can really define 3 bending moments, but in this problem we only need the 1), like this:
##M_A## is taken about one axis, and ##M_x## is taken about another parallel axis displaced from the first axis by a distance ##x##. But when balancing torques, it only makes sense to add torques about the same axis!
I wondered then, why they used two torques about different axes in the same expression? Thanks!
Last edited by a moderator: