- #1
FHbabble
- 2
- 0
I am trying to solve for the deflection and stress in a tapered beam (constant width b)
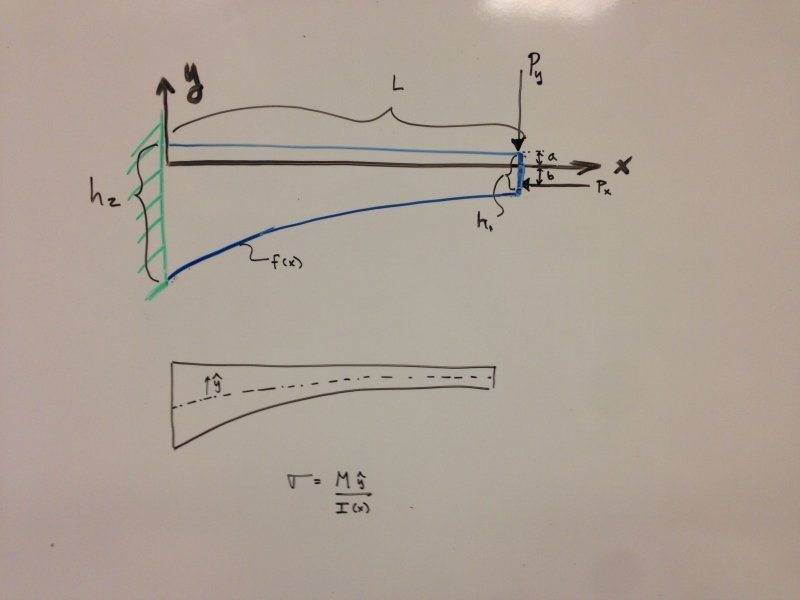 shown in the attachment, and I am getting confused by at least 2 things: 1) how to deal with the "imposed" coordinate system, 2) the nonsymmetric shape and the corresponding neutral axis. [Assume that the bottom taper, f(x), is linear from h1-> h2 for simplicity]
shown in the attachment, and I am getting confused by at least 2 things: 1) how to deal with the "imposed" coordinate system, 2) the nonsymmetric shape and the corresponding neutral axis. [Assume that the bottom taper, f(x), is linear from h1-> h2 for simplicity]
In solving the symmetric tapered beam, it's straight forward enough to put the coordinate system aligned with the neutral axis, formulate the moment(x) from statics, and solve the 4th-order equation. Here, I think the solution y[x] is the displacement of the neutral axis, and the bending stress at a location (x,y) relative to the coord system at the neutral axis ~M(x)*y/I(x).
1) With regards to moving the coordinate system, I tried to solve for the displacement and stress for a simple, straight cantilever bar (length L, width b, height h) with only a vertical load=-P at the end using a coordinate system at the top of the bar and was not able to reconcile the values with the standard result using a coordinate system at the centroid. I was solving:
y1''[x] = P*(x-L)/(E*I1) , I1=bh^3/12 {coord system at centroid of beam}
y2''[x]=P*(x-L)/(E*I2), I2=bh^3/3 {coord system at top of beam}
y2=y1-h/2
2) For the tapered [nonsymm] case, will the neutral axis be curved (maybe following the centroid of the cross section)? Formulating the moment(x) using statics is kind-of a pain, because the internal forces will also contribute to M(x) since they do not go through the "chosen" coordinate system, but at the end of formulating M(x) with respect to the shown coordinate system I am stuck in formulating the differential equation with respect to the neutral axis, similar to my issue stated in 1):
Do I/(How do I) need to calculate the neutral axis for formulating the differential eq for the displacement?
-> How do I calculate the displacement of the top surface of the beam?
Is the stress still M(x)y/I(x), where y is measured from the centroid/neutral axis?
Thank you for taking a look. Your advice on 1) or 2) or both is really appreciated!
In solving the symmetric tapered beam, it's straight forward enough to put the coordinate system aligned with the neutral axis, formulate the moment(x) from statics, and solve the 4th-order equation. Here, I think the solution y[x] is the displacement of the neutral axis, and the bending stress at a location (x,y) relative to the coord system at the neutral axis ~M(x)*y/I(x).
1) With regards to moving the coordinate system, I tried to solve for the displacement and stress for a simple, straight cantilever bar (length L, width b, height h) with only a vertical load=-P at the end using a coordinate system at the top of the bar and was not able to reconcile the values with the standard result using a coordinate system at the centroid. I was solving:
y1''[x] = P*(x-L)/(E*I1) , I1=bh^3/12 {coord system at centroid of beam}
y2''[x]=P*(x-L)/(E*I2), I2=bh^3/3 {coord system at top of beam}
y2=y1-h/2
2) For the tapered [nonsymm] case, will the neutral axis be curved (maybe following the centroid of the cross section)? Formulating the moment(x) using statics is kind-of a pain, because the internal forces will also contribute to M(x) since they do not go through the "chosen" coordinate system, but at the end of formulating M(x) with respect to the shown coordinate system I am stuck in formulating the differential equation with respect to the neutral axis, similar to my issue stated in 1):
Do I/(How do I) need to calculate the neutral axis for formulating the differential eq for the displacement?
-> How do I calculate the displacement of the top surface of the beam?
Is the stress still M(x)y/I(x), where y is measured from the centroid/neutral axis?
Thank you for taking a look. Your advice on 1) or 2) or both is really appreciated!