- #1
LiorSh
- 24
- 0
[Mentors' note: Moved from the technical forums, so no template]
Hi,
I have to find energy levels of an electron in a cylindrical shape. I know how to derive the formula below:
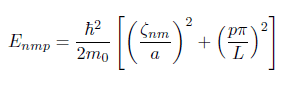
However, I'm not sure which zero value and what intger p I need to use in order to find the lowest energy.
If these are the bessel function zeros:
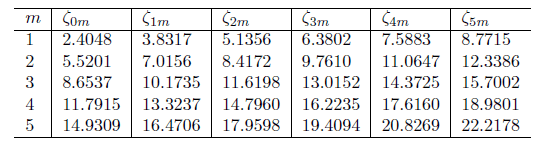
Lets say, I want to find the lowest energy - Do I need to use the value of 2.4048 and p =1 ? What about the second lowest? would I use 5.5201 and p=2?
Thanks!Lior
Hi,
I have to find energy levels of an electron in a cylindrical shape. I know how to derive the formula below:
However, I'm not sure which zero value and what intger p I need to use in order to find the lowest energy.
If these are the bessel function zeros:
Lets say, I want to find the lowest energy - Do I need to use the value of 2.4048 and p =1 ? What about the second lowest? would I use 5.5201 and p=2?
Thanks!Lior
Attachments
Last edited by a moderator: