g.lemaitre
- 267
- 2
Homework Statement
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Homework Statement
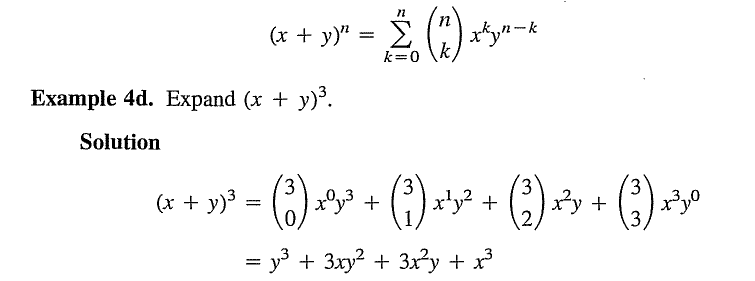
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Hi Infinitum! Call me Georges.
Does that mean you take 3!/2!? That work for the 3rd and 4th term but not for the second term and for the first term I think it's undefined.
The binary coefficient, \displaystyle \binom nk is defined as follows.g.lemaitre said:Homework Statement
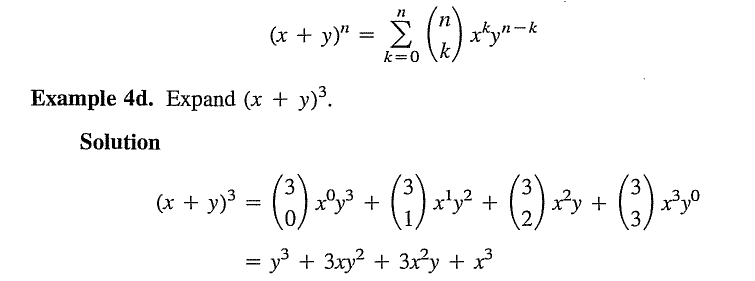
What am I supposed to do with the 3 over 2 in the parentheses? It can be divide and it can be take the factorial. So what do I do with it?
g.lemaitre said:Man, infinitum, you're such a big number it takes me like forever just to count you.
I understand the binomial coefficient and can get the right answer for terms 2 3 and 4 but I'm still having trouble with the first term.
if
\binom{n}{r} = \frac{n!}{r!(n-r)!}
then
\binom{3}{0} = \frac{3!}{0!(3-0)!} = \frac{6}{0}