Biot-Savart Law problem

[Eva01]

Homework Statement

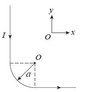
A long (effectively infinite) wire segment
is connected to a quarter of a circular arc with
radius a. The other end of the arc is connected
to another long horizontal wire segment. The
current is flowing from the top coming down
vertically and flows to the right along the pos-
itive x-axis. I have included the image below.
I = 7.5A, a = 0.69 m. Find the magnetic field at O?

Homework Equations

B = μ0 * I / 2a

The Attempt at a Solution

As far as I understand since we only consider the arc part then I use the formula from above but I am not getting the right answer.

B = 4∏ * 10^-7 * 7.5 / 2*0.69 = 6.8295 N/m

 

[gash789]

Hello Eva01,

Firstly you need to consider the origin of your equation :

B = μ0 * I / 2a

which is the Biot Savart law.

$B = \frac{\mu_{0}}{4 \pi}\int \frac{(I dl \times \hat{r})}{ |\vec{r}|^{2}}$

For your system you do only need to use the arc system but you should find out why..

For the arc itself, consider the law above. Clearly the I and the denominator are constant. So we need to solve

$\int (dl \times \hat{r})$

Remembering that a chord (r) connecting the point O to the arc will always be perpendicular to an infinitesimal length of the arc. This should give you a similar equation to what you have been using but it requires an additional factor somewhere.


I would also advise that you check your units at some point.

Hope this helps

 

[Eva01]

Thank you for your help!