hogrampage
- 107
- 1
Homework Statement
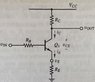
The circuit in the figure has the form of a BJT inverter, but also has a resistor connected between the emitter lead and ground. This addition provides feedback between the output loop of the circuit and its input loop.
(a) Find an exact expression for the Vin-Vout transfer characteristic over the region where Q1 operates in the constant-current region.
(b) To what does your expression reduce to for large βf?
(c) At what value of Vin does Q1 first turn on?
(d) When Q1 saturates, what will be the value of Vout?
(e) At what approximate value of Vin will Q1 first go into saturation?
(f) For VCC = 12V, RC = 4.7kΩ, RE, large βF, Vsat ≈ 0.2V, and Vf ≈ 0.7V, draw the approximate transfer characteristic of the circuit.
(g) The approximate expression obtained in part (b) will overestimate the actual gain of the circuit found in part (a). How large must βF be for the approximation to overestimate the gain by no more than 10%?
Homework Equations
KVL
In the constant-current region:
iC = βFiB
Vout has the form Vout = mVin + b
Vout has the form Vout = mVin + b
The Attempt at a Solution
iE = iB + iC = iB + βFiB = iB(1 + βF)
KVL input loop:
[1] iB = \frac{V_{in} - V_{f}}{R_{B} + R_{E}(1 + β_{F})}
KVL output loop:
[2] Vout = VCC - iCRC - iERE
[3] Vout = VCC - βFiBRC - iBRE(1 + βF)
[4] Vout = VCC - iB(βFRC + RE(1 + βF))
[3] Vout = VCC - βFiBRC - iBRE(1 + βF)
[4] Vout = VCC - iB(βFRC + RE(1 + βF))
Part (a)
If I combine equations [1] and [4]:
[5] Vout = VCC - \frac{V_{in} - V_{f}}{R_{B} + R_{E}(1 + β_{F})}(βFRC + RE(1 + βF))
I want to know if I'm headed in the right direction and where to go from here. Any guidance is greatly appreciated!
Thanks!