Block drifts off between two moving planes through friction

[kekpillangok]

Homework Statement

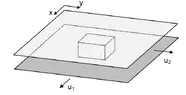
A small brick is compressed between two parallel planes in zero gravity. The planes are perpendicular to the z-axis. The bottom plane is moving with a constant velocity $u _{1 }$ along the x-axis, while the top plane is moving with a constant velocity $u _{2 }$ along the y-axis. Initially, the brick is at rest. The coefficients of kinetic friction between the brick and each plane are identical.

Find the velocity $\vec{v }$ of the brick after a long time for $u _{1 }>u _{2 }$.

Relevant Equations

f = ma
f_friction = mi * N

Here's what I've tried.

$\vec{v }$ is the velocity of the brick after it has stopped changing. I've been able to conclude that this must happen when the relative velocity vectors $\vec{v }-\vec{u }_{1 }$ and $\vec{v }-\vec{u }_{2 }$ lie along the line connecting the tip of $\vec{u }_{1 }$ to the tip of $\vec{u }_{2 }$. One can see this by drawing diagrams like these:

I've already figured out, by examining the forces acting on the brick, that the friction forces have the same magnitude. It follows, then, that, for the friction forces to cancel each other out, they must be aligned as follows:

This forces $\vec{v }$ to point from the origin to the segment connecting the tips of $\vec{u }_{1 }$ and $\vec{u }_{2 }$. I cannot, however, for the life of me, figure out where exactly on that segment $\vec{v }$ will point after a long time has elapsed. I've tried reasoning as follows: at the very first moment after the brick is released, two friction forces of equal magnitude act on it, one pointing in the direction of $\vec{u }_{1 }$ and the other pointing in the direction of $\vec{u }_{2 }$—i.e. the net force makes an angle of 45° with the horizontal, and I thought, at first, that there was no reason why the net force would steer off that angle. However, I found that it does, and now I'm having a hard time figuring things out.

If I can find where the endpoint of $\vec{v }$ lies on the hypotenuse ${\left| \vec{v }-\vec{u }_{1 }\right| }+{\left| \vec{v }-\vec{u }_{2 }\right| }$, the problem becomes one of finding a cevian where the segments into which it divides are more or less determined. At present, I can't see a nice property about this net force, always pointing along the bisector of the relative velocity vectors, that will help me find this endpoint. If anyone can suggest an idea or lend a hand, I will be extremely grateful.

 

[haruspex]

It might be simpler to work in scalars.
If the components of $\vec v$ at some instant are $v_1, v_2$, can you write expressions for their derivatives?

 

[kekpillangok]

It might be simpler to work in scalars.
If the components of $\vec v$ at some instant are $v_1, v_2$, can you write expressions for their derivatives?

Thanks for replying!
I found the following expressions for the derivatives:

$\frac{\, \mathrm{d } \, v _{1 } \, }{\, \mathrm{d } \, t \, }=\frac{f }{m }{\left( \cos \left( \theta _{1 }\right) \, -\cos \left( \theta _{2 }\right) \, \right) }$

$\frac{\, \mathrm{d } \, v _{2 } \, }{\, \mathrm{d } \, t \, }=\frac{f }{m }{\left( \sin \left( \theta _{2 }\right) \, -\sin \left( \theta _{1 }\right) \, \right) }$

They are written in terms of the angles $\theta _{2 }$ and $\theta _{1 }$ between the horizontal and the friction vectors $\vec{f }_{2 }$ and $\vec{f }_{1 }$, as in this image:

I found them by considering Newton's second law component-wise. I can see that integrating the expressions would lead to the components for $\vec{v }$, so I've been trying to find some way to do that.
In particular, I've tried to find some relationship between $\theta _{2 }$, $\theta _{1 }$ and $\theta$, where $\theta$ is the angle that $\vec{v }$ makes with the horizontal, but all my attempts so far have got messy really quickly, with a lot of ugly trigonometry.

I can also see some relationships like $\cos \left( \theta _{2 }\right) \, =\frac{v _{1 }}{\sqrt{{{\left( u _{2 }-v _{2 }\right) }}^{2 }+{v _{1 }}^{2 }}}$ and $\cos \left( \theta _{1 }\right) \, =\frac{u _{1 }-v _{1 }}{\sqrt{{{\left( u _{1 }-v _{1 }\right) }}^{2 }+{v _{2 }}^{2 }}}$ and similar expressions for the sines of these angles. With these, it is possible to eliminate the angles, but the algebra looks awful. I think I'm stuck again. Have I even found the derivatives you were thinking of?

 

[haruspex]

the algebra looks awful

Quite so, and matches what I got.
My next thought was to model it and see if that yields any insights. Haven’t tried it yet.

Update..
modelling suggests to try this:
Suppose at some time $v_2/v_1=u_2/u_1$. What can you say about $\dot v_2/\dot v_1$?

 

[kekpillangok]

Suppose at some time $v_2/v_1=u_2/u_1$. What can you say about $\dot v_2/\dot v_1$?

I'm a bit puzzled. If the particle starts from rest, it seems to me that, at each instant, the acceleration and velocity vectors should be aligned. I'm not sure if this is right. At the very first instant, however, this is certainly the case: both acceleration and velocity make an angle of 45° with the horizontal. If this continues, we can say that, if $v _{2 }/v _{1 }=u _{2 }/u _{1 }$ at some instant, then, at that instant, the ratio should also apply to $\dot{v }_{2 }/\dot{v }_{1 }$.

At that instant, then, the geometry tells us that $\theta =\frac{\pi }{2 }-\frac{{\left( \theta _{2 }+\theta _{1 }\right) }}{2 }$. I didn't find anything else of much use.

I'm struggling to see a nice property about this ratio $u _{2 }/u _{1 }$.

 

[haruspex]

I'm a bit puzzled. If the particle starts from rest, it seems to me that, at each instant, the acceleration and velocity vectors should be aligned. I'm not sure if this is right. At the very first instant, however, this is certainly the case: both acceleration and velocity make an angle of 45° with the horizontal. If this continues, we can say that, if $v _{2 }/v _{1 }=u _{2 }/u _{1 }$ at some instant, then, at that instant, the ratio should also apply to $\dot{v }_{2 }/\dot{v }_{1 }$.

At that instant, then, the geometry tells us that $\theta =\frac{\pi }{2 }-\frac{{\left( \theta _{2 }+\theta _{1 }\right) }}{2 }$. I didn't find anything else of much use.

I'm struggling to see a nice property about this ratio $u _{2 }/u _{1 }$.

Ah, sorry, misread the modelling results. Forget post #4.
What they show, paradoxically, is that as the u1/u2 ratio increases the v1/v2 ratio decreases. Not sure I believe that… maybe I have two equations crossed over.
Here are some sample outputs:

u1/u2	v1/v2
1​	1​
1.1​	0.9643599969​
1.2​	0.9330440907​
1.3​	0.905408294​
1.4​	0.8809100934​
1.5​	0.8590947979​
1.6​	0.8395819709​
1.7​	0.8220531456​
1.8​	0.8062412172​
1.9​	0.7919215177​
2​	0.7789044202​
2.1​	0.7670292607​
2.2​	0.7561593657​
2.3​	0.7461779891​
2.4​	0.7369849933​
2.5​	0.728494133​
2.6​	0.720630828​
2.7​	0.7133303311​
2.8​	0.7065362167​
2.9​	0.7001991291​
3​	0.6942757425​

Anyway, I suggest you use the same approach with your equations to try to get some insight into what the relationship is.

 

[TSny]

What they show, paradoxically, is that as the u1/u2 ratio increases the v1/v2 ratio decreases. Not sure I believe that… maybe I have two equations crossed over.

I think the behavior is to be expected. Just after release, the block will pick up a small velocity in the 45-degree direction as shown by the small orange vector below.

The green vectors w1 and w2 show the velocity of the block relative to the lower plate and upper plate, respectively. The corresponding friction forces f will act opposite to these vectors and have the same magnitude.

θ1 and θ2 are small angles with θ2>θ1. So, the net y-component of the force on the block is greater than the net x-component of the force. Therefore, we expect the block to gain speed in the y-direction faster than in the x-direction.

 

[TSny]

I tried setting up the equations of motion and used Mathematica to solve them numerically. I get similar results to @haruspex 's post #6, but with somewhat smaller values for v1/v2. I could have messed up somewhere.

I

 

[haruspex]

I tried setting up the equations of motion and used Mathematica to solve them numerically. I get similar results to @haruspex 's post #6, but with somewhat smaller values for v1/v2. I could have messed up somewhere.

View attachment 363510

I

Your result is probably more accurate. I modelled it in a spreadsheet with fairly coarse timesteps.

 

[TSny]

I still don't see an analytic solution. The only relation for the final velocity components that I have found is $\large \frac{v_1}{u_1} + \frac{v_2}{u_2} = 1$, which matches @kekpillangok 's geometrical condition that the tip of $\vec v$ must lie on the hypotenuse of the $u_1$ - $u_2$ triangle in the OP.

 

[haruspex]

I still don't see an analytic solution. The only relation for the final velocity components that I have found is $\large \frac{v_1}{u_1} + \frac{v_2}{u_2} = 1$, which matches @kekpillangok 's geometrical condition that the tip of $\vec v$ must lie on the hypotenuse of the $u_1$ - $u_2$ triangle in the OP.

There is an intriguing datapoint in your results: 2.4, 0.72 to a considerable degree of precision.

 

[Lnewqban]

$\frac{\, \mathrm{d } \, v _{1 } \, }{\, \mathrm{d } \, t \, }=\frac{f }{m }{\left( \cos \left( \theta _{1 }\right) \, -\cos \left( \theta _{2 }\right) \, \right) }$

$\frac{\, \mathrm{d } \, v _{2 } \, }{\, \mathrm{d } \, t \, }=\frac{f }{m }{\left( \sin \left( \theta _{2 }\right) \, -\sin \left( \theta _{1 }\right) \, \right) }$

Why is mass showing in these equations if the small brick and the two parallel planes are in zero gravity?

 

[TSny]

Mass is playing the role of inertia here, rather than associated with gravity.

 

[haruspex]

There is an intriguing datapoint in your results: 2.4, 0.72 to a considerable degree of precision.

@TSny, can you confirm these datapoint ratios? Not the individual numbers, just the y/x ratios.

uy	ux	vy	vx
1​	1​	1​	1​
4​	3​	8​	9​
12​	5​	18​	25​
24​	7​	32​	49​

?
If so Pythagoras has something to say.

 

[kekpillangok]

The two forces on the block are $\vec{f }_{1 }$ and $\vec{f }_{2 }$. The net force in the x-direction, therefore, is $f _{1 }\cos \left( \theta _{1 }\right) \, -f _{2 }\cos \left( \theta _{2 }\right) \,$. So, by Newton's second law, $f _{1 }\cos \left( \theta _{1 }\right) \, -f _{2 }\cos \left( \theta _{2 }\right) \, =m \cdot \dot{v }_{1 }$.

I'm sorry if this question will surprise you (I'm a bit of a newbie ), but would either @TSny or @haruspex mind giving an explanation of what this $u _{2 }/u _{1 }$ ratio is that you're analysing numerically? Why is it changing with $v _{2 }/v _{1 }$? I thought, at first, that you were comparing initial values of $u _{2 }$, $u _{1 }$, $v _{2 }$ and $v _{1 }$, but that isn't the case, since $v _{2 }/v _{1 }=1$ for any starting values of u2 and u1.

Edit: You're looking at the final ratios, of course! Never mind the above, haha.

 

[TSny]

@TSny, can you confirm these datapoint ratios? Not the individual numbers, just the y/x ratios.

uy	ux	vy	vx
1​	1​	1​	1​
4​	3​	8​	9​
12​	5​	18​	25​
24​	7​	32​	49​

?
If so Pythagoras has something to say.

Your divination works!

You took ux < uy, but that's ok. [Edited]

 

[haruspex]

Your divination works!

You took ux < uy, but that's ok. [Edited]

So it seems $2v=(\sqrt{1+u^2}-u+1)^2$, where u and v are the two ratios.
But how to prove it?
Maybe we can show that if at some time u and v satisfy that equation then the acceleration components ratio is also v.

 

[TSny]

So it seems $2v=(\sqrt{1+u^2}-u+1)^2$, where u and v are the two ratios.

This formula definitely works. I've tested it with several arbitrary choices of u1 and u2.

I noticed from the numerical solution that the decrease in speed of the block relative to plate 1 (from its initial speed relative to plate 1) equals the decrease in speed of the block relative to plate 2 (from its initial speed relative to plate 2). This holds at any instant of time.

So, the solution appears to follow from the following two statements:

(1) The final velocity of the block relative to plate 1 and the final velocity relative to plate 2 have opposite directions.

(2) The block decreases its speed relative to plate 1 by the same amount relative to plate 2.

The first statement follows easily from the fact that the final net force on the block must be zero.

I'm not yet understanding why the second statement holds.

 

[kekpillangok]

(2) The block decreases its speed relative to plate 1 by the same amount relative to plate 2.

Can we explain this from the fact that, at each instant, there are acceleration vectors of equal magnitude along the directions of the velocities relative to plate 1 and plate 2?

 

[TSny]

Can we explain this from the fact that, at each instant, there are acceleration vectors of equal magnitude along the directions of the velocities relative to plate 1 and plate 2?

Yes. I think that's it!

The two friction forces are represented by f. $\vec W_1$ is the velocity of the block relative to plate 1 and $\vec W_2$ is the velocity relative to plate 2.

It should be clear that Fnet makes the same angle to $\vec W_1$ as it does to $\vec W_2$. So, the rate of change of $|\vec W_1|$ equals the rate of change of $|\vec W_2|$.

 

[haruspex]

So, the rate of change of $|\vec W_1|$ equals the rate of change of $|\vec W_2|$.

Took me a while to get that last step. Need to consider infinitesimal changes, yes? If the magnitude of the velocity change is dv then the change in magnitude of each relative velocity approximates $dv\cos(\theta)$.

 

[TSny]

Took me a while to get that last step. Need to consider infinitesimal changes, yes? If the magnitude of the velocity change is dv then the change in magnitude of each relative velocity approximates dvcos⁡(θ).

Yes. At each instant of time, the speeds W1 and W2 are decreasing at the same rate.

Thus, the overall changes ΔW1 and ΔW2 are equal.