- #1
Tanya Sharma
- 1,540
- 135
Homework Statement
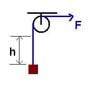
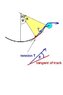
A block of mass 1 Kg initially at rest at point B is being pulled by a constant force F= 100N along a smooth circular track of radius 10 m . Find the velocity of the block when it reaches point P making an angle 60 with the vertical.
Homework Equations
The Attempt at a Solution
KE1+PE1+W[F]=KE2+PE2
Now KE1=PE1=0 assuming reference level to be at B.
KE2=1/2(mv[2]
PE2=mgl(1-cos60°)
W[F]=?
How do we calculate work done by force F? My understanding says that angle between constant force and displacement changes continuously as the block moves along the track.Please help me.Thanks...

 ) Nonetheless, there's a much easier way to solve this and my suggestion stands as is.
) Nonetheless, there's a much easier way to solve this and my suggestion stands as is.