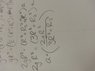Two Toilet Papers dropping-Rotational Inertia

Click For Summary
SUMMARY

The discussion focuses on a physics homework problem involving the comparison of two toilet paper rolls dropped from the same height, one unraveling and the other not. Key equations discussed include the rotational inertia formula, I = M (R - R2)^2, and the conservation of energy equation, mgh = (1/2) Iw^2 + (1/2) Mv^2. Participants emphasize the importance of understanding the differences in potential energy (PE) between the two rolls and the application of Newton's second law to analyze their motion. The final acceleration equations derived are a = (2/3)((gR^2)/(R^2 + R2^2)) for the unraveling roll and a = g for the other roll.

PREREQUISITES
  • Understanding of rotational inertia and its calculation.
  • Familiarity with conservation of energy principles in physics.
  • Knowledge of Newton's second law and its application in rotational motion.
  • Basic algebra skills for manipulating equations and solving for variables.
NEXT STEPS
  • Study the concept of rotational inertia in detail, particularly for cylindrical objects.
  • Learn how to apply conservation of energy to systems involving both linear and rotational motion.
  • Explore the implications of Newton's second law in rotational dynamics.
  • Practice solving similar physics problems involving energy conservation and rotational motion.
USEFUL FOR

Students studying physics, particularly those focusing on mechanics, educators teaching rotational dynamics, and anyone interested in practical applications of energy conservation principles.

CentrifugalKing
Messages
23
Reaction score
0

Homework Statement


Okay, so I'm supposed to take two fresh rolls of toilet paper and drop them. One of which, I am supposed to let unravel while falling. The other, I just drop on its own. I'm supposed to find the height at which both will drop and hit the ground at the same time.

Homework Equations


Rotation Inertia for Toilet Papers: I= M (R-R2)^2

Conservation of Energy: KE1 + PE1 = KE2 + PE2

The Attempt at a Solution



I know that

KE1= 0 and PE2 = 0

So

PE1 = KE2

mgh = (1/2) Iw^2 + (1/2)Mv^2

Okay... this was all I wrote. At this point I realized, that I did not know the difference between the two.

What would make the unraveling toilet paper any different from the one that falls?
 
Physics news on Phys.org
CentrifugalKing said:
What would make the unraveling toilet paper any different from the one that falls?
For one thing, the final PE of the unraveling toilet paper will not be zero. It stretches out as it unravels.
 
Oh so it will be

mgh= (1/2)(M)(Rf)((v^2)/(Rf^2)) +Mv^2 + PE?

So what would PE equal? Would the mass change to just one sheet of paper rather than the whole roll?

Or should I also set up Newton's 2nd Law?
 
CentrifugalKing said:
Or should I also set up Newton's 2nd Law?
That's what I would do. See if you can compare the accelerations.
 
Hate to bump this up again, but I've gotten pretty far but got jumbled on one part.

So I did net torque = I(alpha)

And did some substitution

mg*R = (((1/2)(M) (R^2+R2^2) + MR^2))) (a/R)

Thing is, would

R^2+R2^2 be the same as the other R's?

Sorry if I'm not being clear. But how would the formula play out? I know M cancels.
 
CentrifugalKing said:
Hate to bump this up again, but I've gotten pretty far but got jumbled on one part.

So I did net torque = I(alpha)

And did some substitution

mg*R = (((1/2)(M) (R^2+R2^2) + MR^2))) (a/R)
This looks good. Note: R is the outer radius; R2 is the inner radius.

CentrifugalKing said:
Thing is, would

R^2+R2^2 be the same as the other R's?
Not sure what you mean. See my comment above.

The linear acceleration will be in terms of both R and R2.
 
@Doc Al

Thanks for all your help, and I think I got it.

After a bit of Algebra:

(2/3)((g*R^2)/(R^2+R2^2))=a

And the other a=g

Is that all I can do?

And then compare it?
 
CentrifugalKing said:
After a bit of Algebra:

(2/3)((g*R^2)/(R^2+R2^2))=a
I get something slightly different, so double check your algebra.

CentrifugalKing said:
And the other a=g

Is that all I can do?

And then compare it?
Once you have the two accelerations, figure out how the heights they must be dropped from have to relate for them to fall in the same time. (Hint: for a given distance, solve for the time to reach the ground.)
 
Oh,

So I did a bit.

Is this correct?

I brought the R from a/R to the other side.
I wanted to cancel the 1/2 so I multiplied everything by 2.

2gR^2 = (R^2+R2^2+2R^2) a?
 
  • #10
Oh I see my mistake! So this is right?
 

Attachments

  • 20151202_132851.jpg
    20151202_132851.jpg
    27.3 KB · Views: 539
  • #11
CentrifugalKing said:
Oh,

So I did a bit.

Is this correct?

I brought the R from a/R to the other side.
I wanted to cancel the 1/2 so I multiplied everything by 2.

2gR^2 = (R^2+R2^2+2R^2) a?
This looks better. But simplify the expression within the parenthesis a bit--combine terms.
 
  • #12
CentrifugalKing said:
Oh I see my mistake! So this is right?
Looks good.
 

Similar threads

Heat energy in an inelastic collision
  • · Replies 8 ·
Replies
8
Views
3K
Find kinetic energy from potential energy and moment of inertia?
  • · Replies 2 ·
Replies
2
Views
4K
How High Will the Puck Shoot Up from the Plate?
  • · Replies 27 ·
Replies
27
Views
4K
Block moving on a circular track-Work energy Circular Motion problem
  • · Replies 34 ·
2
Replies
34
Views
6K
High School Mousetrap Car Energy efficiency
  • · Replies 7 ·
Replies
7
Views
789
Rotation of Rigid Bodies: Rotating stick with disc on top
  • · Replies 9 ·
Replies
9
Views
2K
Re: conservation of energy problem(?)
  • · Replies 12 ·
Replies
12
Views
2K
Calculating Moment of Inertia for a Rotating Cylinder | Physics Tutorial
  • · Replies 2 ·
Replies
2
Views
2K
KE and speed of a sphere near a fixed charge
  • · Replies 4 ·
Replies
4
Views
8K
2 masses collide, one has spring. -Collision, Momentum, Spring energy
  • · Replies 3 ·
Replies
3
Views
3K