Block off inclined plane (kinematics + projectile motion?)

[muhammed_oli]

Homework Statement

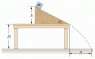
A block of mass m = 2.00 kg is released from rest at h = 0.300 m above the surface of a table, at the top of a θ = 50.0° incline as shown in the figure below. The frictionless incline is fixed on a table of height H = 2.00 m.
a. Find a on the incline
a=7.51 :)

b. Find V(f) on incline
V(f)=2.42 :)

c. How far from the table will the block hit the floor?
:(

d. What time interval elapses between when the block is released and when it hits the floor?
:(

Homework Equations

incline kinematics
y=V(o)t-g/2(t^2)

projectile stuff
t=(2V(o)sin∅)/g
range(x)=(V(o)^2(sin2∅))/g

The Attempt at a Solution

It's free fall kinematics for the plane then projectile for when it falls? I was distracted when he was showing us this

c. range(x)=(2.42^2)sin(100)/g

d. -0.300=0-4.9t^2
t(p)=0.247
t(f)=2(2.42)sin(50)/g
t(f)=0.378
t(tot)=0.247+0.378=0.625 sec

I already missed c but is that how i get there?
Part D wrong.

 

[haruspex]

The range equation you quote for c refers to a certain set-up. What is that set-up? Note that the equation has no input distances, but clearly the height of the table will be important. (It's not much use memorising equations if you don't remember the circumstances in which they apply. I have never bothered memorising many equations, preferring to remember how to use the basic ones.)
So, for c, what are the horizontal and vertical components of velocity when it leaves the ramp?

Your first equation for part d is as though the block falls vertically 0.3m. You already calculated the acceleration down the ramp. What is the vertical component of that?

 

[muhammed_oli]

Hm alright, so the range equation I used was for symmetric projectile motion. I get what you are saying, I seem to mess up once I start using anything beyond the basics.

Okay for C I found the components for final ramp velocity to be 1.56i - 1.85j
v=d/t
Vf=d/t
find t
y=V(o)t-g/2(t^2)
for t? I hate this equation, is there anything easier? I tried a=v/t but wasnt sure of final velocity. edit i think I am barking up the wrong tree with this now.

part d
ramp
5.75m/s^2(y direction)
a=v/t
v=1.85-0
5.75=1.85(t)
t=5.75/1.85

 

[haruspex]

find t
y=V(o)t-g/2(t^2)
for t? I hate this equation, is there anything easier?

That's the one you need.
You could not use v=d/t even if you knew the final speed. Do you know why?

For d, How did you get 5.75 for the vertical component of acceleration down the ramp? (It should be less.)
a=v/t is fine, but that does not seem to be what you did.

 

[muhammed_oli]

part c
v=d/t is for constant velocity?

this is what I am thinking, after I've found t from the other equation
x=v(o)t+(1/2)at^2
a=0
x=v(o)(m/s)t(s)
x=x(m)part d
I used 7.51sin50 to get that answer. I'm not sure how to approach this.

 

[haruspex]

part c
v=d/t is for constant velocity?

yes.

x=v(o)t+(1/2)at^2
a=0
x=v(o)(m/s)t(s)
x=x(m)

Yes.

I used 7.51sin50 to get that answer.

Sorry, my mistake. 5.75 is right. But what you did next was wrong. Try that again.

 

[muhammed_oli]

k, going to solve for t(ramp) using kinematic first.
v(f) = v(o)+at
v(o) = 0
2.42 = 7.51t
t = 0.3222

same, find t for the fall
y = v(o)t-1/2(g)(t^2)
-2 = -1.85t-4.9t^2
4.9t^2+1.85t-2 = 0
t = 0.4774

t(tot) = 0.3222+0.4774 = 0.7996 sec

how does that look?

 

[haruspex]

k, going to solve for t(ramp) using kinematic first.
v(f) = v(o)+at
v(o) = 0
2.42 = 7.51t
t = 0.3222

same, find t for the fall
y = v(o)t-1/2(g)(t^2)
-2 = -1.85t-4.9t^2
4.9t^2+1.85t-2 = 0
t = 0.4774

t(tot) = 0.3222+0.4774 = 0.7996 sec

how does that look?

Looks about right, but you quote too many digits, given the inputs and less precise intermediate results.

 

[muhammed_oli]

thank you beary much! I got it right, 3 sig digits