Solve Bound Charge Question: Griffith's Book Example

[Tony Hau]

Homework Statement

Find the electric field produced by a uniformly polarized sphere of radius R.

Relevant Equations

Potential of a polarized object: $V(\mathbf r) = \frac{1}{4 \pi \epsilon_o} \oint_{S} \frac{\sigma_b}{r}{da} + \frac{1}{4\pi \epsilon_o} \int_V \frac{\rho_b}{r} d{\tau}$

Charged density of bound charge: $\rho_b \equiv - \nabla \cdot \mathbf P$

Surface charge density of bound charge: $\sigma_b \equiv \mathbf P \cdot \hat {\mathbf n}$

This is an example of Griffith's book on bound charge, and the following is the solution to this example.

We choose the z-axis to conincide with the direction of polarization.

By $$\sigma_b \equiv \mathbf P \cdot \hat {\mathbf n} $$ and $$\rho_b \equiv - \nabla \cdot \mathbf P$$ we can see that $\rho_b$ is 0 and $\sigma_b = Pcos\theta$.

The book then gives the solution to the potential without steps, which is: $$V(r,\theta) =
\begin{cases}
\frac{P}{3 \epsilon_o} rcos\theta & \text{for} \text{ }r \leq R \\
\frac{P}{3\epsilon_o}\frac{R^3}{r^2}cos\theta & \text{for } \text{ }r \geq R
\end{cases} $$

This is a figure from the book:

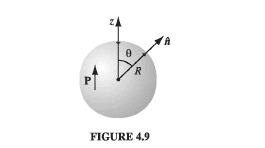
My attempt to the solution is like this:
$$V(\mathbf r) = \frac{1}{4 \pi \epsilon_o} \oint_{S} \frac{\sigma_b}{r}{da} $$, because $\rho_b = 0$.

Then, $\oint_{S} \frac{\sigma_b}{r}da= \int_0^ {\pi}\int_0^{2\pi} \frac{Pcos\theta}{R} R^{2}sin\theta d\theta d\phi$

I think the variable r is a constant because it is integrating over a surface; the r is fixed. However, it is not the case for the solution. Can anyone help?

 

[pasmith]

I don't think the integral formulation will necessarily help you; I believe it should be <br /> V(\mathbf{r}) = \int_S \frac{\sigma_b}{\|\mathbf{r} - \mathbf{r}&#039;\|}\,dS&#039; where the integration is with respect to the primed variable.

I would instead note that since \rho = 0 the potential satisfies \nabla^2 V = 0 in r &lt; R and r &gt; R.

I don't know enough EM to say what boundary condition it must satisfy at r = R due to the charged sphere (presumably Griffiths will tell you), but I suspect that it will end up being a condition of the form \frac{\partial V}{\partial r} = A\cos\theta for some constant A. That would suggest looking for solutions of the form V(r) = f(r) \cos \theta.

 

[Tony Hau]

I don't think the integral formulation will necessarily help you; I believe it should be <br /> V(\mathbf{r}) = \int_S \frac{\sigma_b}{\|\mathbf{r} - \mathbf{r}&#039;\|}\,dS&#039; where the integration is with respect to the primed variable.

I would instead note that since \rho = 0 the potential satisfies \nabla^2 V = 0 in r &lt; R and r &gt; R.

I don't know enough EM to say what boundary condition it must satisfy at r = R due to the charged sphere (presumably Griffiths will tell you), but I suspect that it will end up being a condition of the form \frac{\partial V}{\partial r} = A\cos\theta for some constant A. That would suggest looking for solutions of the form V(r) = f(r) \cos \theta.

The Laplace's equation $\nabla ^{2} V =0$, has the following solution in spherical coordinates: $$V = \sum_{l=0}^{\infty} (A_l r^l + \frac{B_l}{r^{l+1})P_{l}(cos\theta) $$.

The potential boundary condition can be calculated by letting $V_{in} = V_{out}$. But I don't know as well how you can satisfy the boundary condition for this case. The book hasn't mentioned it.

 

[Tony Hau]

I don't think the integral formulation will necessarily help you; I believe it should be <br /> V(\mathbf{r}) = \int_S \frac{\sigma_b}{\|\mathbf{r} - \mathbf{r}&#039;\|}\,dS&#039; where the integration is with respect to the primed variable.

I would instead note that since \rho = 0 the potential satisfies \nabla^2 V = 0 in r &lt; R and r &gt; R.

I don't know enough EM to say what boundary condition it must satisfy at r = R due to the charged sphere (presumably Griffiths will tell you), but I suspect that it will end up being a condition of the form \frac{\partial V}{\partial r} = A\cos\theta for some constant A. That would suggest looking for solutions of the form V(r) = f(r) \cos \theta.

You are totally correct and smart! Thanks.
Here is the solution I have worked out:

The potetial for the interior of the sphere in spherical coordinates is: $$V_{in} = \sum_{l=0}^\infty A_l r^l P_l(cos\theta)$$

By the boundary condition that: $$V_{in} = V_{out}$$ and $$\frac{\partial V_{out}}{\partial r} - \frac{\partial V_{in}}{\partial r} = -\frac{\sigma}{\epsilon_o}$$ at $r=R$, we obtain $$\sum_{l=0}^{\infty}(2l+1)A_l R^{l-1} P_l (cos\theta) = \frac {\sigma}{\epsilon_o}$$ $$= \frac{Pcos\theta}{\epsilon_o}$$

Obviously only the term for $l=1$ survives, and $A_1 = \frac{P}{3\epsilon_o}$.

Subsituting $A_1 = \frac{P}{3\epsilon_o}$ into $V_{in} = \sum_{l=0}^\infty A_l r^l P_l(cos\theta)$, we get $$V_{in}=\frac{P}{3\epsilon_o}r cos\theta$$

 

[pasmith]

Having now checked my copy of Grant & Phillips, it appears that if \mathbf{D}_1 is the field inside the sphere and \mathbf{D}_2 the field outside then at r = R the condition is <br /> (\mathbf{D}_2 - \mathbf{D}_1) \cdot \mathbf{e}_r = \sigma with V continuous. In the absence of volume charge density we have \mathbf{D} = \epsilon_0\mathbf{E} = -\epsilon_0\nabla V.