Boundary conditions of a bending plate

[kosovo dave]

Homework Statement

I'm trying to find the boundary conditions for the following problem:

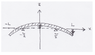
A plate with length 2L is placed on supports at x = L/2 and x = - L/2. The plate is deforming elastically under its own weight (maximum displacement bowing up at x = 0). Both ends of the plate are free boundaries.

The goal is to eventually solve the equation DW'''' = q(x) for the right half of the plate (x > 0).

Homework Equations

D is the flexural rigidity $$\frac{Eh^3}{12(1-\nu^2)}$$

E is Young's Modulus, ν is Poisson's ratio, h is the thickness of the plate, and q = -ρgh.

The Attempt at a Solution

Since the right end of the plate is free, I think the two boundary conditions there are DW''' = 0 (shear force) at x = L and DW'' = 0 (bending moment) at x = L. What are the quantities I should be considering for the boundary conditions at x = 0? I feel like one of them is bending stress.

 

[Chestermiller]

The bending moments and the displacements are zero at both ends. The reaction forces and shear forces are not.

 

[kosovo dave]

By "ends" do you mean of the full plate (x = -L and x = L) or the half-space (x=0 and x = L)? I should also clarify that the ends of the plate (x = +/- L) sag beneath the x-axis.

 

[kosovo dave]

 

[Chestermiller]

View attachment 216419

Oh. I missed this when I was visualizing the system. Yes, the boundary conditions you proposed are the correct ones to use: zero shear force and zero bending moment at both ends.