Bragg diffraction form an “inclined” crystal plane

[crick]

Homework Statement

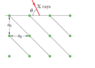
In picture, first-order reflection from the reflection planes shown occurs when an x-ray beam of wavelength $0.260 nm$ makes an angle $\theta=63.8°$ with the top face of the crystal. What is the unit cell size $a_0$?

Homework Equations

Bragg law
$$d=\frac{ n \lambda} {2 \sin \Theta}$$

The Attempt at a Solution

I thought I must consider an angle $\alpha =\theta -45°=18.8°$ in bragg law and then $$a_0=\sqrt{2} \frac{ \lambda} {2 \sin \alpha}$$

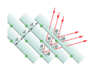
That's because I was sure that the angle of diffraction $\theta$ in bragg's law must always be measured with respect to the plane as in the following picture

Nevertheless I cheked on solution manual found online here : http://omega.altervista.org/extra/key%20to%20Physics.pdf

And I found the following solution:

So the angle used in Bragg law is still $\theta =63.8°$ ! How can it be correct?

 

[Charles Link]

I think you got it right and the book's solution is incorrect, but I would need to double-check my result to be sure.