Discussion Overview
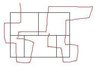
The discussion revolves around a brain teaser involving a geometric problem where participants must determine if a continuous line can be drawn through all sides of a specified arrangement of rectangles without overlapping or retracing any side. The scope includes mathematical reasoning and exploration of graph theory concepts.
Discussion Character
- Exploratory
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants describe the problem as potentially impossible based on the configuration of sides and rectangles, noting that odd-numbered sides complicate the ability to draw a continuous line.
- Others propose that if the problem allows for a continuous curve rather than a strict line, it may be solvable, though this interpretation is contested.
- One participant suggests that alternative methods, such as "punching holes" in the paper, could provide a solution, although this is challenged by others who insist on a strict interpretation of the problem.
- Several participants engage in a detailed analysis of the degrees of vertices in the graph representation of the problem, referencing Euler paths and the conditions for their existence.
- There are claims that the problem resembles classic problems in graph theory, such as the Bridges of Königsberg, and discussions about the implications of these similarities.
- Some participants express frustration over the lack of clarity in the problem's phrasing and the resulting ambiguities that affect the solvability discussion.
- A later reply emphasizes that a more liberal interpretation of the problem might lead to a solution, suggesting that assumptions made by earlier participants could be limiting.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the solvability of the problem. There are multiple competing views regarding the interpretation of the problem and the implications of graph theory on its solution.
Contextual Notes
Limitations include the ambiguity in the problem's phrasing, the definitions of a line versus a continuous curve, and the assumptions about intersections and sides. The discussion also highlights the dependence on the specific arrangement of rectangles and the mathematical properties of the shapes involved.
Who May Find This Useful
Readers interested in mathematical puzzles, graph theory, and geometric reasoning may find this discussion relevant and engaging.