cse63146
- 435
- 0
[SOLVED] Bungee Jumping and Conservation of Energy
A bored college student decides to try bungee jumping. He attaches an elastic bungee cord to his ankles and happily jumps off a tall bridge across a river. He ends up barely touching the water before the cord jerks him back up.
Find the mass of the student m.
Express the student's mass in terms of variables given in the problem introduction and any appropriate constants.
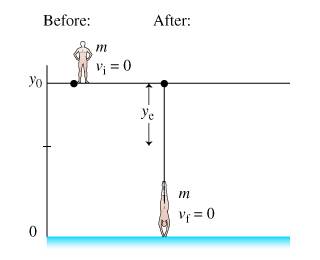

mgy = 0.5KX^{2}
so I get m = (0.5KX^{2})/gy
but this doesn't seem right. Any ideas?
Homework Statement
A bored college student decides to try bungee jumping. He attaches an elastic bungee cord to his ankles and happily jumps off a tall bridge across a river. He ends up barely touching the water before the cord jerks him back up.
Find the mass of the student m.
Express the student's mass in terms of variables given in the problem introduction and any appropriate constants.
Homework Equations
mgy = 0.5KX^{2}
The Attempt at a Solution
so I get m = (0.5KX^{2})/gy
but this doesn't seem right. Any ideas?
Last edited: