shinnsohai
- 41
- 0
I've this to be handed in by tomorrow
Please give some guidelines...
I think that my working is completely wrong !
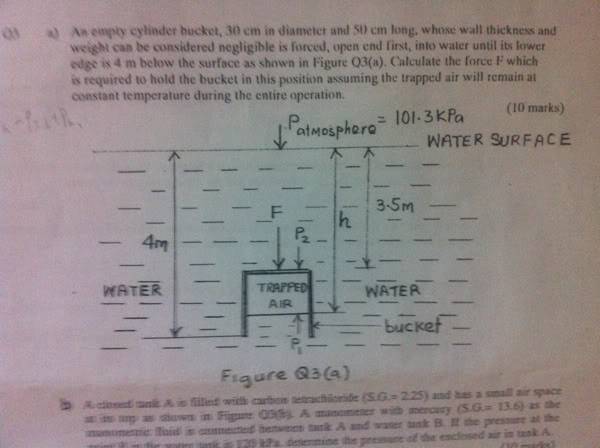
An empty cylinder bucket, 30cm in diameter and 50cm long, whose wall thickness and weight can be considered negligible is forced, open end first, into water until its lower edge is 4m below the surface as shown in the picture. Calculate the force F which is required to hold t he bucket in this position assuming the trapped air will remain at constant temperature during the entire operation.
P=ρ x G x H
P1V1=P2V2
(4-h)ρg(∏(0.15^2))(4-h) = 3.5ρg (∏ (0.15^2))(h-3.5)
(4-h)^2(0.0707)= 3.5(0.0707)(h-3.5)
(16-8h+h^2)(0.0707)= 0.24745h-0.866075
0.0707h^2-0.565h+1.1312= 0.24745h-0.866075
0.0707h^2-0.81305h+1.997275= 0
(3.5ρg+101.3k)∏(0.15^2)(h-3.5)
(4-H)^2ρg(∏(0.15^2))= 3.5ρg(∏0.15^2)(h-3.5)
0.5=h-3.5+4-h
h-3.5=0.5
h=3.5/0.5
h=7
Please give some guidelines...
I think that my working is completely wrong !
Homework Statement
An empty cylinder bucket, 30cm in diameter and 50cm long, whose wall thickness and weight can be considered negligible is forced, open end first, into water until its lower edge is 4m below the surface as shown in the picture. Calculate the force F which is required to hold t he bucket in this position assuming the trapped air will remain at constant temperature during the entire operation.
Homework Equations
P=ρ x G x H
The Attempt at a Solution
P1V1=P2V2
(4-h)ρg(∏(0.15^2))(4-h) = 3.5ρg (∏ (0.15^2))(h-3.5)
(4-h)^2(0.0707)= 3.5(0.0707)(h-3.5)
(16-8h+h^2)(0.0707)= 0.24745h-0.866075
0.0707h^2-0.565h+1.1312= 0.24745h-0.866075
0.0707h^2-0.81305h+1.997275= 0
(3.5ρg+101.3k)∏(0.15^2)(h-3.5)
(4-H)^2ρg(∏(0.15^2))= 3.5ρg(∏0.15^2)(h-3.5)
0.5=h-3.5+4-h
h-3.5=0.5
h=3.5/0.5
h=7
Last edited: