Calc Deflection of Prismatic Beam: Step by Step Guide

In summary, the conversation discusses the process of calculating the deflection of a prismatic beam using superposition. The individual deflections of each part (a, b, and c) must be calculated and then added together to find the total deflection. It is also noted that the angular deflection is assumed to be the same for all three parts. The structure being statically determinate allows for the calculation of loads and deflections at each end. The process involves considering the deflections and rotation caused by bending and rigid body motion.
  • #1
Retros
1
0
Hello PF,

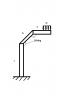
First time here posting. So I have a question about trying to calculate the deflection of this prismatic beam by hand using superposition. I know I can figure it out in SolidWorks, but I also want to know I would do it by hand, or at least the general process. The angled bar b is really throwing me off.

So when calculating the total deflection, δT, at end of bar a, is it the sum of the deflections due to beam a, b, and c?


Can I assume the angular deflection, θ, are the same for bars a, b, and c?
 

Attachments

  • beam1.png
    beam1.png
    1.3 KB · Views: 534
Engineering news on Phys.org
  • #2
The structure is statically determinate, so you can find the loads on the end of each part.

If you start with part a, the loads on the top end are a compressive force and a bending moment, so you can find the deflections and the rotation.

Then at the other end of part b, you have the deflections caused by part b bending, plus the rigid body motion because the end of part a has moved and rotated.

Similarly for part c.
 

Related to Calc Deflection of Prismatic Beam: Step by Step Guide

1. What is the purpose of calculating the deflection of a prismatic beam?

The purpose of calculating the deflection of a prismatic beam is to determine the amount of bending that occurs when a load is applied. This is important in structural engineering as it ensures that the beam is strong enough to support the intended load without breaking or buckling.

2. How do I calculate the deflection of a prismatic beam?

The deflection of a prismatic beam can be calculated using the formula: d = (5WL^4)/(384EI), where d is the deflection, W is the applied load, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia.

3. What factors affect the deflection of a prismatic beam?

The deflection of a prismatic beam is affected by several factors, including the applied load, the length of the beam, the material properties, and the shape and size of the cross-section of the beam.

4. Why is it important to calculate the deflection of a prismatic beam?

Calculating the deflection of a prismatic beam is important because it ensures that the beam is strong enough to support the intended load without causing any structural failure. It also helps engineers to determine the appropriate size and shape of the beam for a specific application.

5. What are some common methods for calculating the deflection of a prismatic beam?

There are several methods for calculating the deflection of a prismatic beam, including the double integration method, the moment-area method, and the conjugate beam method. Each method has its own advantages and may be more suitable for different types of beams and loading conditions.

Similar threads

What is the best beam design for my aluminum tandem axle trailer?
    • Mechanical Engineering
Replies
33
Views
3K
Choosing correct steel beam for a span
    • Mechanical Engineering
Replies
8
Views
2K
Leaf Spring Deflection: Calculating Force & Displacement
    • Mechanical Engineering
Replies
4
Views
3K
How to take a moment into account for deflection of a beam
    • Introductory Physics Homework Help
Replies
8
Views
1K
Calculate Deflection for Aluminium Tube Beam - Inertia, Mass & δ
    • Mechanical Engineering
Replies
4
Views
2K
Bucklig: deflection at Euler load
    • Mechanical Engineering
Replies
3
Views
1K
Second moment of inertia for a bent rectangle
    • Mechanical Engineering
Replies
7
Views
2K
How do you calculate Stress of a curved beam?
    • Mechanical Engineering
Replies
2
Views
3K
Engineering Torsion and deflection of a rectangular beam
    • Engineering and Comp Sci Homework Help
Replies
13
Views
3K
Calculating Angular Deflection in a Welded Steel Bracket
    • Engineering and Comp Sci Homework Help
Replies
11
Views
2K

Hot Threads

Recent Insights

Back
Top