Calc. Thermal Deflection for Alum. Sleeve & Steel Beam

[Dell]

given an aluminium sleeve with a steel beam inside as seeen in the diagram below

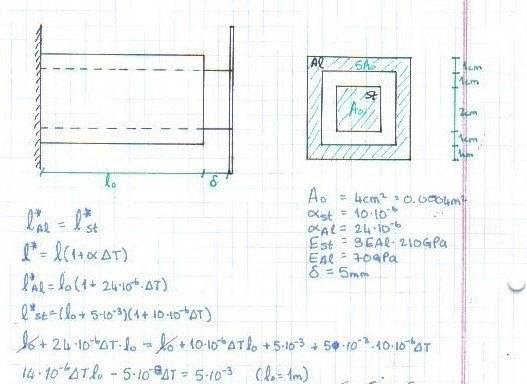
knowing that the length of the steel beam is 5mm longer than the sleeve and that a rigid plate is connected to the end of the steel beam,

find the change in temperature needed to be able to connect the sleeve to the plate?

i base my answer on the assumption that when T=T_f

L_Al=L_St

L^Al=L_o(ΔT*α_Al+1)
L^St=(L_o + 0.005)(ΔT*α_St+1)after comparing i find that my expression for ΔT is dependent on L_o, but L_o, the original length of the sleeve, was not given in the question

is there any way to solve this without knowing L_o?? is there a way i can find L_o?

 

[ponjavic]

What happens if you divide the first equation with the second?

 

[Dell]

that is more or less what i did

but I am still going to have Lo in my equation

 

[ponjavic]

I would say it is not possible and I cannot see anything you've done wrong.

I'd say it's logical that it would depend on the initial length due to 5mm being a fixed value.

Imagine L0 being 1e-10m. An large deltaT would be required. With L0 being extremely large, the opposite would apply.

Agree?

 

[nvn]

Lo is a given parameter. You would, of course, solve for deltaT in terms of Lo.

 

[Dell]

no, Lo isn't a given parameter, i added it in the hope that it would cancel out

 

[nvn]

And what makes you think a given parameter must be a specific numeric value, instead of a variable? Why not solve for deltaT?

 

[Dell]

JUST because all the other values were numerical