mathlearn
- 331
- 0
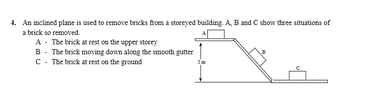
View attachment 6143
Calculate the velocity of the brick at the bottom of the inclined plane.
State the assumption you made for your calculation in part above.
& Sketch the displacement-time graph relevant to the movement of the brick along the smooth gutter. (Assume that the brick started to move from the state of rest.)
Workings:
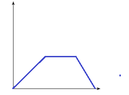
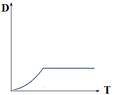
I am unable to think on the first two but I think the displacement and time graph should be something like ,
View attachment 6144
Many Thanks :)
Calculate the velocity of the brick at the bottom of the inclined plane.
State the assumption you made for your calculation in part above.
& Sketch the displacement-time graph relevant to the movement of the brick along the smooth gutter. (Assume that the brick started to move from the state of rest.)
Workings:
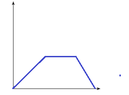
I am unable to think on the first two but I think the displacement and time graph should be something like ,
View attachment 6144
Many Thanks :)