SUMMARY
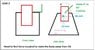
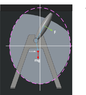
The discussion focuses on calculating the force required to rotate a 4 kg body from 0° to 90° in 5 seconds, considering two cases: one with the force acting at the center of gravity (CG) and another with the force acting away from the CG. In Case 1, the torque is calculated using the equation T = I x α, leading to a force of approximately 1.884 N. In Case 2, the challenge lies in applying the parallel axis theorem to find the moment of inertia, which is not provided in the problem statement. The participants emphasize the importance of understanding the shape and mass density distribution of the body to accurately calculate the required force.
PREREQUISITES
- Understanding of torque and angular acceleration in rotational dynamics
- Familiarity with the parallel axis theorem for moment of inertia calculations
- Knowledge of basic physics equations related to rotational motion
- Ability to interpret and analyze 3D shapes and their mass distribution
NEXT STEPS
- Learn how to calculate moment of inertia for irregular shapes
- Study the application of the parallel axis theorem in detail
- Explore the relationship between torque, force, and angular acceleration in rotational systems
- Investigate the effects of mass distribution on rotational dynamics
USEFUL FOR
Students and professionals in physics, mechanical engineering, and robotics who are involved in rotational dynamics and require a deeper understanding of force calculations related to center of gravity and moment of inertia.