Lambda96
- 233
- 77
- Homework Statement
- Calculate ##\displaystyle{\lim_{x \to 0}} \frac{\cos(x)}{\sin(x)}##
- Relevant Equations
- none
Hi,
I need to check whether the limit of the following function exists or not
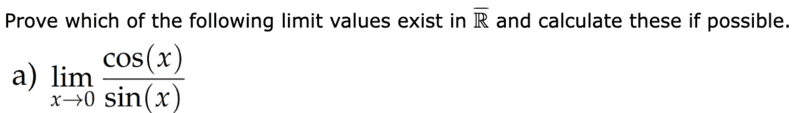 I have now proceeded as follows to look at the right-sided and left-sided limit i.e. ##\displaystyle{\lim_{x \to 0^{+}}}## and ##\displaystyle{\lim_{x \to 0^{-}}}##
I have now proceeded as follows to look at the right-sided and left-sided limit i.e. ##\displaystyle{\lim_{x \to 0^{+}}}## and ##\displaystyle{\lim_{x \to 0^{-}}}##
To do this, I drew up a list in which I move from 1 closer and closer to 0 and for the left-hand side from -1 towards 0 and got the following:

As you can see, the function tends from the right towards ##\infty## and from the left towards ##- \infty## As the two values are therefore not equal, the function has no limit at the point ##x=0##
My question, can I prove it this way, or is there a way to prove it more precisely mathematically?
I need to check whether the limit of the following function exists or not
To do this, I drew up a list in which I move from 1 closer and closer to 0 and for the left-hand side from -1 towards 0 and got the following:
As you can see, the function tends from the right towards ##\infty## and from the left towards ##- \infty## As the two values are therefore not equal, the function has no limit at the point ##x=0##
My question, can I prove it this way, or is there a way to prove it more precisely mathematically?
