Calculating Area of Polar Function: Spiral r = 5(e^.1θ)

[klarge]

1. Problem: Use the spiral r = 5(e^.1θ). Find the area of the region in Quadrant I that is outside the second revolution of the spiral and inside the third revolution.



2. Homework Equations :

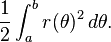
3. Attempt at solution:

My problem with finding the area of a polar graph is determining the bounds, so to get the right bounds for this graph do I set the equation equal to zero? I am really at a loss as to how to set up the bounds. Any hints would be helpful.

 

[jhicks]

So... the second revolution is between which values of $\theta$ and the third is between which values of $\theta$? $\theta = 0$ is the start of the first.

 

[klarge]

2nd between -2pi and 2pi and the third between -4pi and 4pi?

 

[jhicks]

One full revolution is $2\pi$ radians. If revolution 1 is for $0 < \theta < 2\pi$ and the second revolution starts at $\theta = 2\pi$ radians and spans $2\pi$ subsequent radians, the second revolution has what range of $\theta$?.

 

[klarge]

$2\pi < \theta < 4\pi$
and the third would be $4\pi < \theta < 6\pi$.

 

[jhicks]

Correct.

 

[klarge]

So the bounds would be between $2\pi < \theta < 4\pi$?