Finding area enclosed by the polar curve

[Coderhk]

Homework Statement

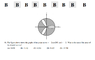
Question attached in attachments

Homework Equations

Area enclosed by polar graph is ∫0.5r^2
where r is the radius as a function of angle theta

The Attempt at a Solution

I attempted to use the formula above and I subtracted the area of the inside from the outside but it seems to yield an incorrect solution.

$0.5∫((2cos(3x))^2)dx-0.5∫4dx$
The limit of integration are from $0$ to $2π$

The answer is D

 

[andrewkirk]

integrating from 0 to $2\pi$ without adjustment is no good. There are at least two problems with that:

1. The three-leaved flower shape is traversed twice as the integration variable travels from 0 to $2\pi$. So there is double-counting going on.

2. $r$ is negative for half the time, which will give negative integrals.

Instead I suggest, to get the area of the three-leaved shape, you instead integrate over half a leaf, for instance from 0 to $\pi/6$. If you do that then $r$ is never negative over that range, and every part of the area is covered only once. Then multiply the area you get by six to get the total area of all three identical leaves. Then take that away from the area of the circle.

 

[epenguin]

I don't think either of points 1 and 2 of #2 are correct. r is squared so there is no negative. And from 0 to 2π is going round the circle once isn't it?
True you don't have to integrate around the whole circle, you could integrate around a third of it with any lower limit you like, or in the upper limit you like as long as the difference between them is 2π/3 - then multiply by 3.

For your answer you give no indications of what you got wrong. Area enclosed by polar graph is ∫0.5r^2dθ . For the shaded area you have got the signs wrong. For the area of the whole disk, I think you could be allowed to use a well-known formula! Then compare with your calculation to see you got everything right.

 

[Coderhk]

I don't think either of points 1 and 2 of #2 are correct. r is squared so there is no negative. And from 0 to 2π is going round the circle once isn't it?
True you don't have to integrate around the whole circle, you could integrate around a third of it with any lower limit you like, or in the upper limit you like as long as the difference between them is 2π/3 - then multiply by 3.

For your answer you give no indications of what you got wrong. Area enclosed by polar graph is ∫0.5r^2dθ For the shaded area you have got the signs wrong. For the area of the whole disk, I think you could be allowed to use a well-known formula! Then compare with your calculation to see you got everything right.

I tried integrating from 0 to #pi/6# and then multiplied it by 6. Afterwards I got the area using pi*R*R and subtracted the white space using the result I got in the first step. I solved it already but thank you very much