Calculating Chemical Potential from Energy Derivatives

[GravityX]

Homework Statement

Show that for a fluid column the chemical potential as a function of height can be written as follows $\mu_h=\mu_0+mgh$

Relevant Equations

none

Hi

Unfortunately, I can't get on with the following task.

The system looks like this

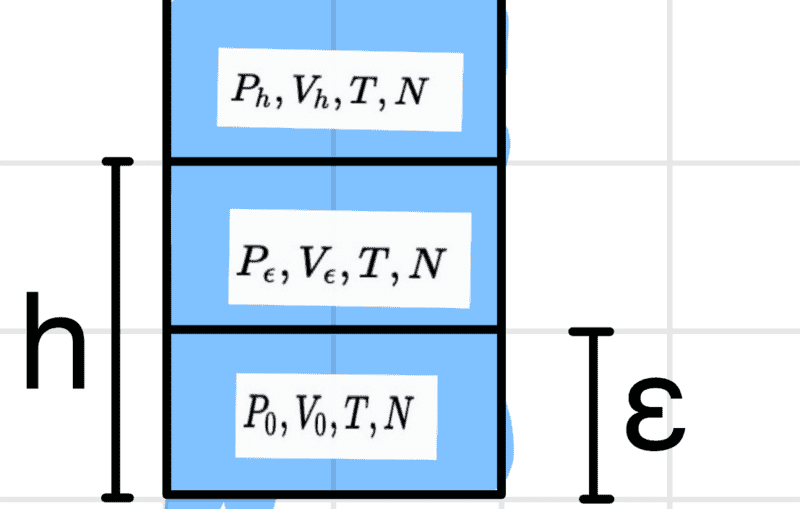
it is divided in such a way that the same number of particles is present in each $\epsilon$ section. I am now to determine the energy $E(P_h,V_h,N)$ at the height h using the energy $h=0$ i.e. $E_0(P_h,V_h,N)$ and with this I am then to derive the above equation for the chemical potential.

I would now have simply derived the energy using the hydrostatic pressure equation $P=\rho gh+P_0$ by simply multiplying the equation by the volume $V_h$, i.e. $PV_h=\rho ghV_h+P_0V_h=mgh+P_0V_h=U_h+U_0$.

Now I'm getting nowhere, unfortunately, because to get the chemical potential I would have to derive the energy according to N, so $\mu=\frac{\partial U}{\partial N}$ unfortunately there is no N in the above equation.

 

[Chestermiller]

Are you dealing with the chemical potential of a component in an ideal gas mixture?

 

[GravityX]

The task only says fluid (gas or liquid), so it is not explicitly mentioned. It then goes on to say

The fluid is in equilibrium, homogeneous in temperature, and consists of one type of particle with mass m

 

[Chestermiller]

Well, at constant temperature, $$\frac{d\mu}{dP}=V$$For an ideal gas, this becomes: $$\frac{d\mu}{dP}=\frac{RT}{P}$$Furthermore, for an ideal gas, from the baratropic equation, $$\frac{dP}{dh}=-\rho g=-\frac{PM}{RT}$$where M is the molecular weight.

 

[GravityX]

Thanks Chestermiller for your help , your derivation also helped me with the second task