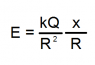Calculating Electric Field from a Dipole: Is This Equation Accurate?
- Thread starter novelriver
- Start date
Click For Summary
SUMMARY
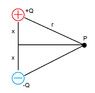
The discussion centers on the accurate calculation of the electric field (\(\vec E\)) at a point \(P\) from a dipole. The correct formula for the electric field is derived as \(E = 2kQx/r^3\), where \(k\) is Coulomb's constant, \(Q\) is the charge, \(x\) is the horizontal distance, and \(r\) is the distance from the dipole. Participants emphasized the importance of vector addition and correctly identifying the components of the electric field, clarifying that the x-components cancel while the y-components do not in this context.
PREREQUISITES- Understanding of electric fields and dipoles
- Familiarity with vector addition in physics
- Knowledge of trigonometric functions in relation to physics problems
- Basic grasp of Coulomb's law and its constants
- Study the derivation of electric fields from dipoles in detail
- Learn about vector components and their significance in physics
- Explore Coulomb's law and its applications in electrostatics
- Practice problems involving electric fields and dipole configurations
Students of physics, educators teaching electrostatics, and anyone interested in mastering the concepts of electric fields and dipole interactions.
Similar threads
- · Replies 11 ·
- · Replies 10 ·
- · Replies 25 ·
- · Replies 2 ·