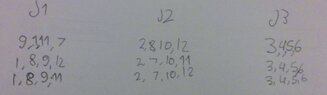bio said:
In the Gadsden Diving Championships there is a panel of three judges. There are 12 scorecards with the numbers 1-12 on them, which are distributed so that each judge has four. After the diver has performed their routine, the judges each hold up a score card, and the diver's score is the sum of the three scorecards added together.
So, my question is:
What are all the different ways that the cards can be distributed among the judges, if all player scores from 6-29, except 10, were possible? Also, explain why ithere's no other way of distributing the scorecards. (other than swapping sets of 4 scorecards between judges)
Working Out:
I've already worked out some combinations, such as
Are there any others? Thanks!
Interesting problem! It probably helps if you are familiar with
Kakuro puzzles.
Your first solution is wrong, because it does not give any way to show a score of $11$. Your other two solutions are correct, and I believe that there are also four other solutions.
Start by looking at how to achieve the small scores. There is only one way to get $6$, namely $1+2+3$. So each of the scorecards for $1$, $2$ and $3$ must be allocated to a separate judge. As in your solutions, let's agree that $1$ goes to Judge 1, $2$ to Judge 2, and $3$ to Judge 3.
Similarly, $7$ has to be $1+2+4$. So $4$ must go to Judge 3. There are two ways to express $8$, namely $1+3+4$ and $1+2+5$. But $3$ and $4$ are already both with the same judge, so the only available combination for $8$ is $1+2+5$, and therefore $5$ must also go to Judge 3.
Of the various combinations for $9$ (which any Kakuro player would know instantly), the only one available is $1+2+6$. So $6$ must go to Judge 3, whose collection is now complete.
There are now no ways to get the score $10$ without using two of the scorecards held by Judge 3. To get the score $11$, there is only one remaining possibility, namely $1+3+7$. So $7$ must go to Judge 2.
Now look at the highest scores. The only possibility for $29$ (given that Judge 3 has nothing higher than a $6$) is $6+11+12$. So $11$ and $12$ must go to different judges. That just leaves the scorecards $8$, $9$ and $10$. Any one of these can go to Judge 2, with the other two going to Judge 1. That leaves six possible solutions, as follows: $$\begin{array}{ccc}\text{Judge 1} & \text{Judge 2} & \text{Judge 3} \\ \hline 1,9,10,11 & 2,7,8,12 & 3,4,5,6 \\ 1,8,10,11 & 2,7,9,12 & 3,4,5,6 \\ 1,8,9,11 & 2,7,10,12 & 3,4,5,6 \\ 1,9,10,12 & 2,7,8,11 & 3,4,5,6 \\ 1,8,10,12 & 2,7,9,11 & 3,4,5,6 \\ 1,8,9,12 & 2,7,10,11 & 3,4,5,6 \end{array}$$
Notice that for every combination of scorecards from Judges 1 and 2, you obtain a sequence of four consecutive scores by adding either $3$, $4$, $5$ or $6$ from Judge 3. That cuts down considerably on the amount of work involved in checking that each of these solutions works.