Metalsonic75
- 28
- 0
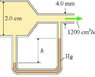
Air flows through this tube at a rate of 1200 cm^3/sec. Assume that air is an ideal fluid.
What is the height h of mercury (in cm) in the right side of the U-tube?
In case the picture doesn't show up, the tube is a Venturi tube. Wide end has diameter of 2cm, narrow diameter is 4 mm, and velocity of the air exiting the tube is 1200 cm^3/sec. The mercury is higher in the u-tube section directly below the narrow segment, and I need to find the height difference of the mercury on the right and left sides.
I've tried using the velocity equations for a venturi tube: v_1 = A_2*sqrt[(2rho*gh)/rho(A_1^2 - A_2^2)] and solving for h. I also tried using the equation p_1 + 0.5rho*v_1^2 = p_1 - rho*gh + 0.5rho(A1/A2)^2*v_1^2 and solving for h.
I'm not getting the right answers. I got something like 6.40cm for the first method, and 8.31cm. To obtain the velocity in the larger part of the tube I used A1v1=A2v2
and got 48 cm^3/sec.
I also have no idea what to do with all of these units. Should I leave all of my measurements in centimeters (2 cm, 1200cm^3/sec, etc) or in meters (0.02m, 12 m^3 sec, etc.) I might be getting the right answer, and be off by a factor of 100. How can I calculate the h?
I appreciate your time.
What is the height h of mercury (in cm) in the right side of the U-tube?
In case the picture doesn't show up, the tube is a Venturi tube. Wide end has diameter of 2cm, narrow diameter is 4 mm, and velocity of the air exiting the tube is 1200 cm^3/sec. The mercury is higher in the u-tube section directly below the narrow segment, and I need to find the height difference of the mercury on the right and left sides.
I've tried using the velocity equations for a venturi tube: v_1 = A_2*sqrt[(2rho*gh)/rho(A_1^2 - A_2^2)] and solving for h. I also tried using the equation p_1 + 0.5rho*v_1^2 = p_1 - rho*gh + 0.5rho(A1/A2)^2*v_1^2 and solving for h.
I'm not getting the right answers. I got something like 6.40cm for the first method, and 8.31cm. To obtain the velocity in the larger part of the tube I used A1v1=A2v2
and got 48 cm^3/sec.
I also have no idea what to do with all of these units. Should I leave all of my measurements in centimeters (2 cm, 1200cm^3/sec, etc) or in meters (0.02m, 12 m^3 sec, etc.) I might be getting the right answer, and be off by a factor of 100. How can I calculate the h?
I appreciate your time.