Calculating if a Pipe Clamp will slip

[SteveGlow]

Hi,

First, I want to thank ahead of time any help that can be provided. Second, I'm just an advanced tinker'r needing help on a project.

Description:
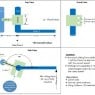
-Lever 1 and Clamp are attached
-Lever 2 and Rod 2 are attached.
-Clamp is tightened around Rod 2
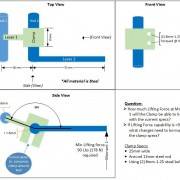
-Upward force on end of Lever 2 needs to be at least 90 lbs without Clamp slipping.

What I've tried to do:
1. Calculate the Clamping Force using the equation from:(https://www.engineersedge.com/calculators/torque_calc.htm)
Bolt Major Dia: .3125"
Coef Friction: .2 (steel)
Calculated Axial bolt clamp force = 800 lbs

2. Calculate the Needed Clamping Force using the equation in posting:
(https://www.physicsforums.com/threads/determining-the-clamping-force-on-a-tube.558240/)
F_clamping X Radius_tube = F_applied X Larm or
F_Clamping = (F_applied X Larm) / Radius_tube
= (50 lbs x 2.756") / .237"
= 581.435 lbs
Summary:
Since the Clamping Force of 800 lbs exceeds the needed F_Clamping of 581 lbs, this scenario should be successful.

Is all of this correct?

I do wonder if the 160 deg angle affects this. Also, how does the contact square area of the clamp come into play on frictional force?

Thanks Again!

 

[Merlin3189]

I find your calculations a bit confusing.

You seem to find the axial tension in the bolt (or bolts ?) to be 800 lb force. I haven't checked this. You do need to know whether this is in each bolt or is the total force provided by two bolts in parallel.

Then you calculate (I think) the needed clamping torque of the clamp on rod 2, by equating it to the torque applied by a 50 lb force on rod 1. I haven't checked this either, because your calculation is in inches, when the diagram dimensions are in mm.
I don't know where the 50 lb force on rod 1 is obtained from. It's not marked on the diagram nor stated in the problem description. I hope you're not getting confused with the "50 psi" torque applied to the bolts? (Which should be 50 lb inches or some such.)

On your diagram you state,"Min lifting force 90 lb (178 N) required".
Neither value appears in your calculation and you should note that 90 lb force ≠ 178 N, so which is the min required?

On the other hand the angle between input and output torques does not matter, UNLESS the forces applied are not perpendicular to the arms.

Perhaps you can clarify the problem. And maybe make what you are calculating, with what values, obtained from where, a bit clearer.

 

[JBA]

I don't know about other industry applications, but, in the petroleum industry pipe clamps alone are not used to restrict the forces or movements longitudinal to the pipeline. One solution is to weld a collar to the pipe that rests against the pipe clamp.