TheArrow
- 8
- 3
- TL;DR
- Solving for RoC of a plane when T/W, L/D, and forward velocity are provided
Hello everyone,
I'm trying to solve a problem from a textbook suggested by a fellow member here:
To help me visualize the problem, I made the diagram below (not necessarily to scale or accurate, just an organizational aid):
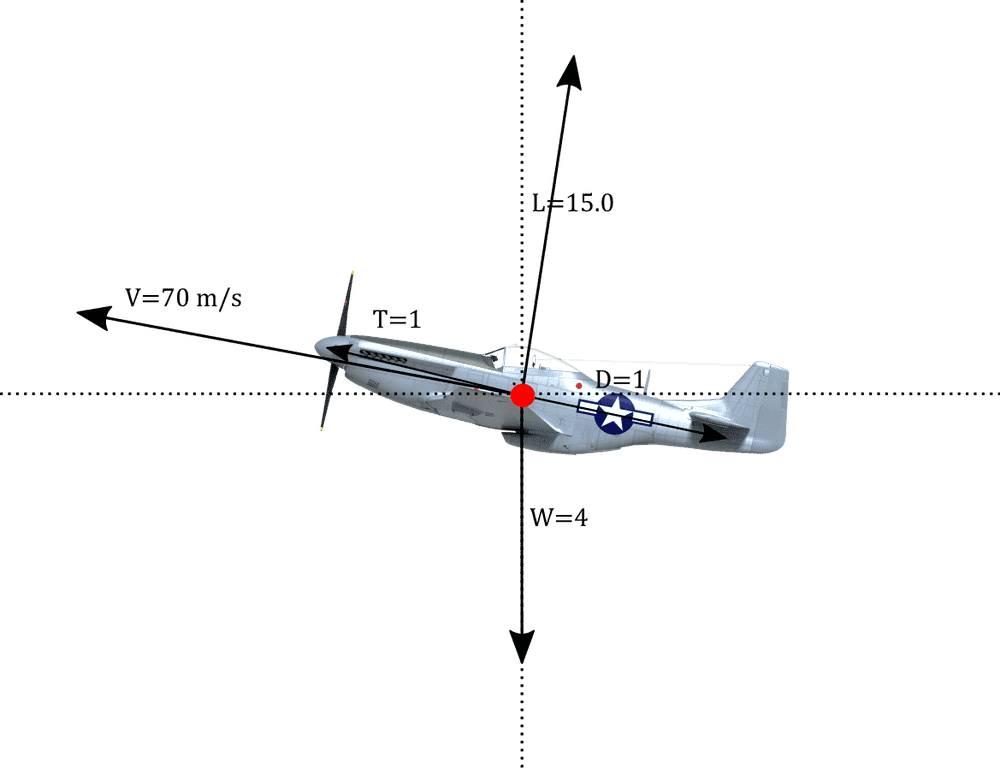
The textbook gives a simplified equation of ##\theta_{c}=\frac{T-D}{W}## (Call it Equation 1.0) to solve for the angle of climb. If I substitute the values from the simplified fractions of ##\frac{T}{W}=\frac{1}{4}## and ##D=1## (from ##\frac{L}{D}=\frac{15}{1}##), the climb angle comes out to be 0 degrees. Because ##T-D=0##.
Another equation is provided to get the power available: ##P_{avail}=TV## (Equation 1.1). Since ##T=1##, ##P_{avail.}=70##.
##P_{req'd}=DV##. Substituting in ##D=1##, results in ##P_{avail.}=70##.
The equation for the rate of climb of theta finally is ##W(V\theta{c})=P_{avail.}-P_{req'd}##. The text says this equation is derived from "multiplying through" (some clarification on what this term means in this context would be helpful), Equation 1.0. Which in this case, the solution would be 0 m/s. Which is in line with the solution to Equation1.0 (in that if the angle of climb is 0 degrees, it would have 0 m/s rate of climb since it isn't climbing). But this doesn't seem right (I suspect I need to solve for the real values of T, W, D, and L rather than the simplified fractions, but I'm not sure how). The text doesn't provide a solution so I have nothing to compare my work to so I have no real feedback on whether I'm approaching this correctly.
Hopefully someone with a bit more familiarity with this can give some feedback.
Thanks in advance!
I'm trying to solve a problem from a textbook suggested by a fellow member here:
Calculate the Rate of Climb of an airplane having a thrust-to-weight (##\frac{T}{W}##) ratio of 0.25 and a lift-to-drag ratio (##\frac{L}{D}##) of 15.0 at a forward velocity of 70 m/s (230 fps). Express ##V_{c}## in ##m/s##.
To help me visualize the problem, I made the diagram below (not necessarily to scale or accurate, just an organizational aid):
The textbook gives a simplified equation of ##\theta_{c}=\frac{T-D}{W}## (Call it Equation 1.0) to solve for the angle of climb. If I substitute the values from the simplified fractions of ##\frac{T}{W}=\frac{1}{4}## and ##D=1## (from ##\frac{L}{D}=\frac{15}{1}##), the climb angle comes out to be 0 degrees. Because ##T-D=0##.
Another equation is provided to get the power available: ##P_{avail}=TV## (Equation 1.1). Since ##T=1##, ##P_{avail.}=70##.
##P_{req'd}=DV##. Substituting in ##D=1##, results in ##P_{avail.}=70##.
The equation for the rate of climb of theta finally is ##W(V\theta{c})=P_{avail.}-P_{req'd}##. The text says this equation is derived from "multiplying through" (some clarification on what this term means in this context would be helpful), Equation 1.0. Which in this case, the solution would be 0 m/s. Which is in line with the solution to Equation1.0 (in that if the angle of climb is 0 degrees, it would have 0 m/s rate of climb since it isn't climbing). But this doesn't seem right (I suspect I need to solve for the real values of T, W, D, and L rather than the simplified fractions, but I'm not sure how). The text doesn't provide a solution so I have nothing to compare my work to so I have no real feedback on whether I'm approaching this correctly.
Hopefully someone with a bit more familiarity with this can give some feedback.
Thanks in advance!