SUMMARY
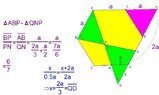
The discussion focuses on calculating the ratio of segments $\overline{BP}$ to $\overline{PN}$ in a regular hexagon $ABCDEF$. Points $M$ and $N$ are defined as the midpoints of sides $\overline{CD}$ and $\overline{DE}$, respectively. The intersection point $P$ is formed by the lines $\overline{AM}$ and $\overline{BN}$. The established ratio is determined through geometric properties and relationships inherent in regular hexagons.
PREREQUISITES
- Understanding of regular hexagon properties
- Knowledge of midpoint theorem
- Familiarity with geometric intersections
- Basic algebra for ratio calculations
NEXT STEPS
- Study the properties of regular hexagons in geometry
- Learn about the midpoint theorem and its applications
- Explore geometric intersection techniques
- Practice ratio calculations in geometric contexts
USEFUL FOR
Students of geometry, mathematics educators, and anyone interested in advanced geometric problem-solving techniques.