NewtonianAlch
- 453
- 0
Homework Statement
Evaluate the follow by first changing the order of integration
\int_{x=-1}^{1}\int_{y=x^2}^{2-x^2}dydx
The Attempt at a Solution
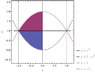
This is the region we're concerned with:
http://www.wolframalpha.com/input/?i=plot%28y%3Dx^2%2C+y+%3D+2+-+x^2%2C+x%3D+1%2C+x%3D+-1%29
The new inequalities would be:
0 ≤ y ≤ 2
\sqrt {-y+2} ≤ x ≤ √y
\int_{y=0}^{2}\int_{x=sqrt(-y + 2)}^{sqrt(y)}dxdy
Doing this double integral gives me a final answer of zero which I checked on MAPLE. The correct answer is 8/3
I'm guessing the bounds are incorrect, but I can't figure out why. On the plot y clearly has a lower limit of 0 and an upper limit of 2. The limits of x I just manipulated through the previous inequality.