Calculating the digits of pi by colliding boxes

[Frodo]

TL;DR

Calculating the digits of pi by colliding boxes

I came across this and it is rather fun!

Assume there is a floor and a wall. There is a 1 lkg box on the left and a box to its right as shown in the diagram. Assume there is no friction and that no energy is lost during any collision.

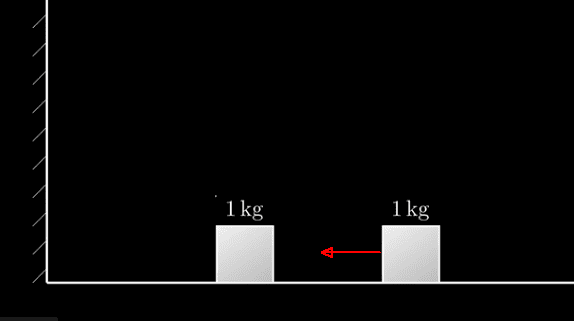
Set the right box to 1 kg and cause it to move to the left until it collides with the 1 kg box. It stops and the left box is pushed to the wall where it bounces off, collides with the right box and stops. The right box travels off to the right. Count the total number of collisions: there are 3.

Repeat by setting the right box to 100 kg; 10,000 kg; 1,000,000 kg ..., etc. We have:

Set the right box to 1 kg and count the collisions: there are 3
Set the right box to 100 kg and count the collisions: there are 31
Set the right box to 10,000 kg and count the collisions: there are 314
Set the right box to 1,000,000 kg and count the collisions: there are 3141

Each time you increase the right box by 100x, you generate an additional digit of pi.

The demonstration and the proof are given at The most unexpected answer to a counting puzzle and the referenced explanation videos.

 

[fresh_42]

See: https://www.physicsforums.com/media/pi-emerging-from-collisions.6259/

I guess the convergence can be called awful.

 

[Frodo]

In a somewhat similar vein, David Bailey and colleagues discovered in 1995 a formula for calculating the Nth digit of pi without calculating the preceding digits. See Finding the N-th digit of Pi which says

By "somewhat similar" is mean that the method similarly allows one to ignore later terms so as to force the integer answer as does the colliding boxes problem.

 

[phinds]

Summary:: Calculating the digits of pi by colliding boxes

Astounding! I never would have believed it. Thanks for posting.

EDIT: for other readers of this thread, the real fun is in the follow-on videos which dig into the math:

Part 2 (15 minutes)
Part 3 (14+ minutes)