Calculating the Specific Heat of a Solution with NaCl and H2O

[joaquinjbs]

It's possible to calculate the latent heats of fusion and the specific heat of a solution of H2O and NaCl?

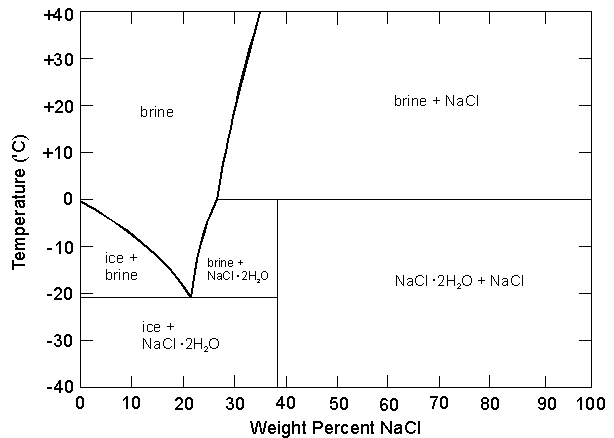
In some cases, it would have two latent heats of fusion? For example, at 10% NaCl, one at -21ºC and another at -5ºC?

Thanks!

 

[DrDu]

Yes, the heat of fusion will be a function of the concentration of the brine.

 

[joaquinjbs]

Thank you DrDu. I guess that heat of fusion will be at -21ºC, but If I have 10% of NaCl, would I have another different heat of fusion at -5ºC, or it would be the same?

 

[BvU]

In some cases, it would have two latent heats of fusion? For example, at 10% NaCl, one at -21ºC and another at -5ºC?
Thanks!

With a 10% solution there is no NaCl formation at either of these two temperatures. The heat of fusion comes into the calculation only on the line between brine and brine + NaCl .

 

[joaquinjbs]

With a 10% solution there is no NaCl formation at either of these two temperatures. The heat of fusion comes into the calculation only on the line between brine and brine + NaCl .

Well, thank you BvU. But for me it's interested what happened on the left of eutectic point. I could calculate the latent heat of fusion of ice+brine?

 

[BvU]

You form ice and the composition moves towards the eutectic point when cooling further.

 

[DrDu]

You can do so, at least for 0% concentration. For very small concentrations, the chemical potential of water in the liquid phase follows Raoult's law $\mu_l(T,x)=\mu_{l0}(T)+RT \ln(x)$ where x is the molar fraction of water in brine. Pressure is constant, so I don't mention it any further. The chemical potential of the solid phase, which consists of pure ice, is $\mu_s(T)$ and depends only on temperature. Now on the melting curve, $\Delta G=\mu_l(T,x)-\mu_s(T)=0$. We can now use a Taylor expansion for $\mu(T,x)$ around $\mu(T_0,1)$, where $T_0$ is the melting point of pure ice. We know that $\partial \Delta G/\partial T|_{P,x}=\Delta S=\Delta H/T_0$ and $\partial \Delta G/\partial x|_{T_0,P}=-RT_0 (1-x)$. So $0=\Delta G=(\Delta H/T_0)\cdot \Delta T -RT(1-x)$ or
$\Delta H=RT_0^2(1-x)/\Delta T$. In the calculation of x, you have to take into account that NaCl will dissociate into sodium and chloride ions.

 

[joaquinjbs]

You can do so, at least for 0% concentration. For very small concentrations, the chemical potential of water in the liquid phase follows Raoult's law $\mu_l(T,x)=\mu_{l0}(T)+RT \ln(x)$ where x is the molar fraction of water in brine. Pressure is constant, so I don't mention it any further. The chemical potential of the solid phase, which consists of pure ice, is $\mu_s(T)$ and depends only on temperature. Now on the melting curve, $\Delta G=\mu_l(T,x)-\mu_s(T)=0$. We can now use a Taylor expansion for $\mu(T,x)$ around $\mu(T_0,1)$, where $T_0$ is the melting point of pure ice. We know that $\partial \Delta G/\partial T|_{P,x}=\Delta S=\Delta H/T_0$ and $\partial \Delta G/\partial x|_{T_0,P}=-RT_0 (1-x)$. So $0=\Delta G=(\Delta H/T_0)\cdot \Delta T -RT(1-x)$ or
$\Delta H=RT_0^2(1-x)/\Delta T$. In the calculation of x, you have to take into account that NaCl will dissociate into sodium and chloride ions.

Ok, thank you very much!

 

[joaquinjbs]

You can do so, at least for 0% concentration. For very small concentrations, the chemical potential of water in the liquid phase follows Raoult's law $\mu_l(T,x)=\mu_{l0}(T)+RT \ln(x)$ where x is the molar fraction of water in brine. Pressure is constant, so I don't mention it any further. The chemical potential of the solid phase, which consists of pure ice, is $\mu_s(T)$ and depends only on temperature. Now on the melting curve, $\Delta G=\mu_l(T,x)-\mu_s(T)=0$. We can now use a Taylor expansion for $\mu(T,x)$ around $\mu(T_0,1)$, where $T_0$ is the melting point of pure ice. We know that $\partial \Delta G/\partial T|_{P,x}=\Delta S=\Delta H/T_0$ and $\partial \Delta G/\partial x|_{T_0,P}=-RT_0 (1-x)$. So $0=\Delta G=(\Delta H/T_0)\cdot \Delta T -RT(1-x)$ or
$\Delta H=RT_0^2(1-x)/\Delta T$. In the calculation of x, you have to take into account that NaCl will dissociate into sodium and chloride ions.

I have been thinking about this all day, but I'm not able to resolve the problem. If you don't mind, could you show me an example?

Than you.

 

[DrDu]

Basically, the final result I derived is the formula for freezing point depression. Every book on physical chemistry should contain a discussion.

 

[joaquinjbs]

Basically, the final result I derived is the formula for freezing point depression. Every book on physical chemistry should contain a discussion.

Thank you, but I'm going to do with an practical experiment. Even so I'll try to resolve the formula.

 

[DrDu]

A first step would be to convert weight percent to molar fraction.

 

[joaquinjbs]

You can do so, at least for 0% concentration. For very small concentrations, the chemical potential of water in the liquid phase follows Raoult's law $\mu_l(T,x)=\mu_{l0}(T)+RT \ln(x)$ where x is the molar fraction of water in brine. Pressure is constant, so I don't mention it any further. The chemical potential of the solid phase, which consists of pure ice, is $\mu_s(T)$ and depends only on temperature. Now on the melting curve, $\Delta G=\mu_l(T,x)-\mu_s(T)=0$. We can now use a Taylor expansion for $\mu(T,x)$ around $\mu(T_0,1)$, where $T_0$ is the melting point of pure ice. We know that $\partial \Delta G/\partial T|_{P,x}=\Delta S=\Delta H/T_0$ and $\partial \Delta G/\partial x|_{T_0,P}=-RT_0 (1-x)$. So $0=\Delta G=(\Delta H/T_0)\cdot \Delta T -RT(1-x)$ or
$\Delta H=RT_0^2(1-x)/\Delta T$. In the calculation of x, you have to take into account that NaCl will dissociate into sodium and chloride ions.

Well I'm back! I would like to resolve this exercise so...

For example, applying this formula to a solution with 10 wt% NaCl (0.17 mol NaCl), which has a T₀ = 268 K, ΔT = 1 K and R = 8.31 J/(molK); I have ΔH = 495392 J

Now with n = 1 mol, and ΔT = 1 K:
Cp = ΔH/(nΔT) = 495392 J/(molK) → 8470*10³ J/(KgK)

So this would be the specific heat of a solution with 10 wt% NaCl in water at -5 ºC. But this huge number has no sense... something I'm doing wrong, could you help me?