Calculating Velocity of Reflected Image in Concave Mirror

[Saitama]

Homework Statement

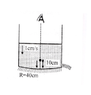
Water level in the tank is decreasing at a constant rate of 1 cm/s. A small metal sphere is moving downwards with a constant velocity of 5cm/s. Base of the tank is a concave mirror of radius 40 cm. Find the velocity of the image seen (refractive index of water=4/3)
a)directly
b)after reflection at the mirror

(Answer: a)4 cm/s downwards (b) 59/4 cm/s upwards)

Homework Equations

The Attempt at a Solution

Honestly I don't know where to start with for (a). The water level isn't stationary here. I tried something random but that gives an incorrect result.
Let x be the height of water level above the mirror and y the height of sphere from mirror. The real depth of sphere is (x-y). The apparent depth is $3/4(x-y)$, differentiating with respect to t, $3/4(dx/dt-dy/dt)=3/4\times 4=3 cm/s$ which is wrong.

Any help is appreciated. Thanks!

 

[Simon Bridge]

I'd probably work it out via the matrixes and put in x-vt for the object position and d-ut for the thickness of the water. The first one just looks like an apparent depth problem.

 

[Saitama]

I'd probably work it out via the matrixes and put in x-vt for the object position and d-ut for the thickness of the water. The first one just looks like an apparent depth problem.

Matrixes? I have never used them in Optics.

 

[TSny]

Let x be the height of water level above the mirror and y the height of sphere from mirror. The real depth of sphere is (x-y). The apparent depth is $3/4(x-y)$, differentiating with respect to t, $3/4(dx/dt-dy/dt)=3/4\times 4=3 cm/s$ which is wrong.

Does "rate of change of apparent depth" represent a velocity with respect to the observer or with respect to the surface of the water?

 

[Saitama]

Does "rate of change of apparent depth" represent a velocity with respect to the observer or with respect to the surface of the water?

With respect to observer?

 

[TSny]

What is the definition of apparent depth? Would you be able to indicate apparent depth on a diagram?

 

[Saitama]

What is the definition of apparent depth? Would you be able to indicate apparent depth on a diagram?

I don't know how to define the apparent depth but I can indicate that on a diagram.

 

[TSny]

Is apparent depth measured from the observer to the image or from the surface of the water to the image?

 

[Saitama]

Is apparent depth measured from the observer to the image or from the surface of the water to the image?

From the surface of water.

 

[TSny]

From the surface of water.

Yes

At any instant of time, how could you write an expression for the distance from the observer to the image in terms of the apparent depth?

 

[Saitama]

Yes

At any instant of time, how could you write an expression for the distance from the observer to the image in terms of the apparent depth?

Assuming that the height of observer from the surface of water is h, the distance is $h+3/4(x-y)$. Differentiating this and substituting values gives the correct result.

I will be trying the b) part tomorrow morning. Its getting late here. :)

 

[Simon Bridge]

Matrixes? I have never used them in Optics.

Never mind, you can just use the formulae for apparent depth and for a concave mirror.
Ray Transfer Matrix analysis is often useful for composite systems ... but, the way your problem is worked, it's probably easier to just do it directly.

It's the same as normal, but positions are functions of time.
Could you use the position formula and just differentiate it wrt time?

 

[Saitama]

Okay, I tried the (b) part but I am getting a wrong result.

The position of image is below the mirror at a distance of 20 cm from mirror. The speed of image is 20 cm/s. If x is the height of water level above mirror and y is the distance of image from the mirror, then apparent depth is 3/4(x+y). Distance of image from observer is h+3/4(x+y). Differentiating w.r.t time, i.e $dh/dt+3/4(dx/dt+dy/dt)=1+3/4(1-20)=-53/4 cm/s$.

 

[TSny]

$dh/dt+3/4(dx/dt+dy/dt)=1+3/4(1-20)=-53/4 cm/s$.

Is $x$ increasing or decreasing with time?

 

[Saitama]

Is $x$ increasing or decreasing with time?

Got it! Thanks!