SUMMARY
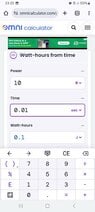
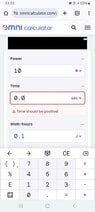
The discussion focuses on calculating watt-hours for time intervals less than one second, specifically using a power of 10 watts over 0.01 seconds. The calculation results in 0.1 joules, which is incorrectly referred to as "J watts hours." The correct conversion from joules to watt-hours involves multiplying by the conversion factor of 1 hour over 3600 seconds, yielding approximately 27.8 micro watt-hours (µWh). The ambiguity in the online physics calculator's interface regarding negative values and unit representation is also highlighted.
PREREQUISITES
- Understanding of basic physics concepts such as power, time, and energy
- Familiarity with unit conversions, specifically from joules to watt-hours
- Knowledge of the formula E = P × t (Energy = Power × Time)
- Experience using online physics calculators for energy calculations
NEXT STEPS
- Research the conversion between joules and watt-hours in detail
- Learn about the implications of using time intervals less than one second in energy calculations
- Explore the functionality and limitations of various online physics calculators
- Study the significance of energy units in practical applications, such as battery capacity
USEFUL FOR
Physics students, electrical engineers, and anyone involved in energy calculations or using online calculators for power and energy assessments.