- #1
ronaldinho52
- 8
- 0
Dear all,
I am stuck with the problem which is given below;
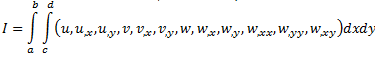
In this problem the equilibrium equations of the given functional must be derived in u, v, and w directions from which the boundary terms must be found. I think that i have derived the equilibrium equations( 5 equations), but i don't know how to proceed. Does anyone maybe know how to do it??
Thanks in advance,
I am stuck with the problem which is given below;
In this problem the equilibrium equations of the given functional must be derived in u, v, and w directions from which the boundary terms must be found. I think that i have derived the equilibrium equations( 5 equations), but i don't know how to proceed. Does anyone maybe know how to do it??
Thanks in advance,