Calculation of absorption spectra

[roam]

I am trying to plot the absorption curve of a given sample using some spectrophotometric data. The data that I've collected are transmittance $T$ and reflectance $R$ – the ratios of transmitted and reflected light power to incident light power. However, using two different methods I got two very different answers:

(1) When radiation impinges on a material, we know that:

$$R+A+T=1 \tag{1}$$

Therefore, if we have obtained $R$ and $T$ using a spectrophotometer, then we can simply solve for $A$ and plot the results.

(2) Most textbooks define absorbance (sometimes called optical density, OD) as:

$$A=\log_{10}\left(\frac{1}{T}\right) \tag{2}$$

If we know $T$ using a spectrophotometer then we can plot absorption using Eq. 2.

Here are my results from both methods. The top curve is calculated using Eq. 1 (dashed/dotted lines are $T$ and $R$). The bottom curve was calculated using Eq. 2 (but the answer had to be multiplied by 100 so that it appears as a percentage).

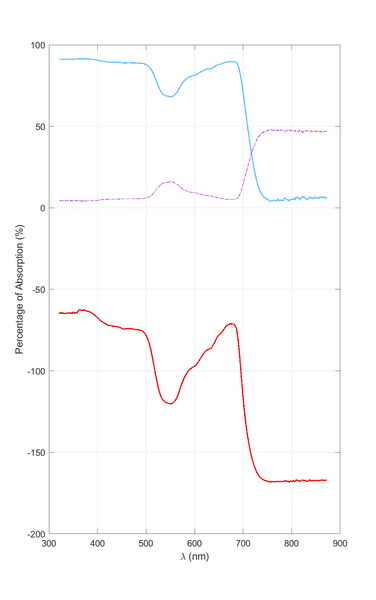
So, which is the correct method and why?

Also, using the second approach we get negative values for absorption (on the ordinate of the graph). How is this usually solved in the post-processing?

Any suggestions would be greatly appreciated.

 

[Lord Jestocost]

One has to distinguish between absorptance and absorbance. Have a look at section 2.2.2.1 in [PDF]Introduction to Optical Characterization of Materials - Springer

 

[roam]

I see. So to plot an absorption spectrum one has to use absorptance (Eq. 1)?

Clearly, absorptance gives the actual amount that is deposited in the material (absorption) by subtracting all the transmitted/reflected/scattered light. I know that absorbance (Eq. 2) is derived by assuming an exponential attenuation. This quantity is described (e.g. in your link) as the density of the material or the amount of attenuation the light receives. Which method would be more appropriate for comparing the absorption characteristics of two different samples?

 

[Lord Jestocost]

I would always prefer to compare "internal absorbances". The internal absorbance A_int is related to the internal transmittance T_int by
A_int = - log10(T_int).
The internal transmittance is defined as the ratio of the radiant power transmitted by the sample to the incident radiant power, fully corrected for reflection losses and any window absorption. Regarding the spectroscopic nomenclature have a look at Applied Spectroscopy Spectroscopic Nomenclature - SAGE Publishing